| Startseite | Glossar | Gästebuch | Forum | Impressum | FAQ | Inhalt |
| |
|
Seitenanfang | Seitenende |
"Ostern fällt auf den Sonntag nach dem Frühlingsvollmond", so lautet stark vereinfachend die Regel für die Bestimmung des Osterdatums. Damit ein Jahr das gleiche Osterdatum hat wie ein Vergleichsjahr müssen zwei Voraussetzungen gegeben sein:
1.: Wochentagskalender:
Bei jedem Jahreswechsel verschiebt sich der Wochentagskalender um einen Tag, in Schaltjahren nach dem 29. Februar um einen weiteren Tag.
In 5 Jahren verschiebt sich der Wochentagskalender um 7 Tage oder eine Woche, wenn in diesen 5 Jahren zwei Schalttage zu liegen kommen. Dies ist immer dann der Fall, wenn das Ausgangsjahr ein Jahr vor einem Schaltjahr liegt, also in 25% aller Fälle, so zum Beispiel in den Jahren 2007 / 2012 oder 2011 und 2016. eine Serie kann hier nicht entstehen.
In 6 Jahren verschiebt sich der Wochentagskalender um 7 Tage oder eine Woche, wenn in diesen 6 Jahren ein Schalttag liegt. Dies ist immer dann der Fall, wenn das Ausgangsjahr ein Schaltjahr ist oder ein Jahr, das auf ein Schaltjahr folgt. Dies trift zu in 50% aller Fälle, so zum Beispiel in den Jahren 2000/ 2006 oder 2001 / 2007. Eine Serie kann hier ebenfalls nicht entstehen.
In 11 Jahren verschiebt sich der Wochentagskalender um 14 Tage oder um zwei Wochen, wenn in diesen 11 Jahren drei Schalttage liegen. Dies ist immer dann der Fall, wenn das Ausgangsjahr kein Schaltjahr ist, also in 75% aller Fälle. Wählt man als Ausgangspunkt ein Jahr, das direkt vor einem Schaltjahr liegt, so wird vier Mal im Abstand von je 11 Jahren der gleiche Wochentagskalender gelten.
2.: Der Frühlingsvollmond:
Das Datum des Frühlingsvollmonds wird nicht astronomisch berechnet, es folgt vielmehr einem 19jährigen Zyklus. Es gibt immer nur 19 Daten für die Luna XIV, den 14. Tag des Ostermonats, wie dieser Vollmondtag von den Computisten genannt wurde. Im julianischen Kalender lag im im ersten Zyklusjahr die Luna XIV auf dem 5. April. Jedes Jahr wich dann dieser Vollmondtag um 11 Tage zurück. Fiel er auf ein Datum vor dem 21. März, musste der folgende Vollmondtag 30 Tage später herangezogen werden. Beim Übergang vom 19. zum 1. Zyklusjahr schritt man 12 Tage zurück, um wieder auf das Ausgangdatum zurückzukommen. Dieset zusätzliche Tag wurde "saltus lunae", Mondsprung, genannt. Bei Einführung des gregorianischen Kalenders wurde dieses Prinzip beibehalten, allerdings verschieben sich nun die 19. Daten für den Frühlingsvollmond mit den zusätzlichen Schaltungen in den Jahrhundertjahren. Derzeit, das ist in den Jahren 1900 bis 2099, fällt im ersten Zyklusjahr die Luna XIV auf den 14. April.
In 5 Jahren verschiebt sich die Luna XIV um 5 mal 11 gleich 55 Tage. Das ist 5 Tage weniger als zwei Zyklen zu je 30 Tagen. Liegt in diesen 5 Jahren ein Saltus Lunae so verschiebt sich die Luna XIV um 4 Tage.
In seltenen Fällen wiederholt sich ein Osterdatum somit nach 5 Jahren. Die folgende Tabelle zeigt Beispiele aus dem Zeitraum von 1983 bis 2023. In der obersten Reihe das Jahr, darunter der Ostertag und in der untersten Reihe das zu diesem Jahr gehörende Datum der Luna XIV:
|
|
|
|
||||||||||||||||||||||||
In 6 Jahren verschiebt sich die Luna XIV um 6 mal 11 gleich 66 Tage. Das ist 6 Tage mehr als zwei Zyklen zu je 30 Tagen. Liegt in diesen 6 Jahren ein Saltus Lunae so verschiebt sich die Luna XIV um 7 Tage oder eine ganze Woche. In seltenen Fällen kann sich ein Osterdatum somit nach 6 Jahren wiederholen. Dies geschah zuletzt in den Jahren 1968 / 1974 , 1981 / 1987, 1988 / 1994 und wird sich das nächste Mal wieder ereignen in den Jahren 2076 / 2082.
|
|
|
|
||||||||||||||||||||||||
In 11 Jahren verschiebt sich die Luna XIV um 11 mal 11 gleich 121 Tagen. Das heisst, dass sich die Luna XIV, zieht man vier vollständige Zyklen zu je 30 Tagen ab, um einen Tag verschiebt, oder aber um zwei Tage, falls innert dieser 11 Jahre ein Saltus Lunae liegt. So verschiebt sich die Luna XIV innerhalb jener 44 Jahre, in den der gleiche Wochenkalender gilt, insgesamt mindesten um vier und höchstens um fünf Tage. Liegt im Ausgangsjahr der Frühlingsvollmond kurz vor dem Ostersonntag, wird Ostern in allen vier Jahren auf das gleiche Datum fallen, liegt er dagegen im Ausgsngsjahr weit vor dem Ostersonntag, wird das Osterdatum nach 11 Jahren bereits um eine Woche zurückweichen.
Somit wird innerhalb dieser 44 Jahre Ostern vier Mal, drei Mal oder je zwei Mal auf das gleiche Datum fallen.
|
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||
Zusammenfassung
Wie man sieht, kann der Ostersonntag nach fünf oder sechs Jahren wieder auf den gleichen Tag fallen, allerdings nur je ein Mal. Im Abstand von jeweils elf Jahren wird sich das Datum des Osterfestes zwei, drei oder nicht selten auch vier Mal wiederholen
In Griechenland wurde 1923 der gregorianische Kalender eingeführt. Er wurde 1924 auch von der orthodoxen Kirche übernommen. Alle unbeweglichen Feiertage richten sich nach diesem Stil. Das Osterdatum wird in Griechenland jedoch weiterhin nach dem alten Stil berechnet, also nach dem Modus, der im Abendland bis 1582 galt. (siehe Das Datum des Osterfestes)
Um das Osterdatum für Griechenland zu ermitteln, muss daher im Osterrechner der alte Stil gewählt werden. Das so ermittelte Datum ist dann in den neuen Stil umzurechnen. Für die Jahre 1900 - 2099 müssen 13 Tage addiert werden. Für diese Umrechnung kann natürlich auch der Kalenderrechner benutzt werden. (Eingabe: julianisch, Ausgabe: gregorianisch)
Beispiel: Für das Jahr 2002 erhält man als Osterdatum nach dem alten Stil den 22. April. Rechnet man dieses Datum in den gregorianischen Kalender um so kommt man auf den 5. Mai. Im Jahr 2002 wird also in Griechenland Ostern am 5. Mai gefeiert.
Das Programm Ostern in Griechenland erspart diese Umrechnungen.
Ostern ist ein kirchliches Fest, demzufolge bestimmen die Kirchen die Festlegung des Osterdatums. Für die katholische Kirche geschah dies durch die von Papst Gregor XIII. verfertige Bulle "Inter gravissimas" vom 24. Februar 1582. In den protestantischen Staaten Deutschlands wurde (nach Experimenten mit einer astronomischen Berechnung des Osterdatums) die Einführung des "Allgemeinen Reichskalenders" durch kaiserliches Patent vom 7. Juni 1776 beschlossen. Dies war die facto die Übernahme der Reform Gregors XIII. durch die evangelischen Stände, man scheute sich allerdings noch lange, das Wort "gregorianisch" in den Mund zu nehmen. Weitere Ausführungen zu dieser Frage finden Sie in der Abhandlung Das Datum des Osterfestes.
Da sind Sie hier genau richtig! In dem Programm Ostersuche geben sie einen Tag vor, der zwischen dem 22. März und dem 25. April liegen muss. Sie können dann ablesen, wann der Ostersonntag auf diesen Datum fällt. Weitere Osterrechner finden Sie in dem Abschnitt Berechnung des Osterdatums finden Sie zwei Rechner.
Diese Frage zu beantworten ist gar nicht so einfach. In der Literatur findet man unterschiedliche Darstellungen. Am häufigsten ist zu lesen, der Meton´sche Zyklus von 19 Jahren bilde die Grundlage der Osterberechnung, einige Autoren vertreten jedoch die Auffassung, man müsse den Zyklus des Kallippos von 76 Jahren heranziehen, und auf Internetseiten, die von Institutionen der Orthodoxen Kirchen ins Netz gestellt wurden, findet sich sogar die Meinung, die Ost-Kirchen würden Ostern aufgrund des Meton'schen Zyklus berechnen, die West-Kirchen hingegen den Zyklus des Kallippos nutzen.
Zuerst einmal die Fakten:
Meton: Im Jahre 433 v. Chr. veröffentlichte der Astronom Meton, Sohn des Pausanias, seinen neunzehnjährigen Zyklus, der davon ausgeht, dass 19 Sonnenjahre gleich seien mit 235 synodischen Monaten. Meton nahm an, die Dauer seines Zyklus betrage 6940 Tage. Demzufolge hatte nach ihm das Sonnenjahr eine Dauer von 365 Tagen, 6 Stunden und knapp 19 Minuten. Auch die Dauer des synodischen Monats war zu hoch angesetzt.
Kallippos: Um das Jahr 334 v. Chr. kam Kallippos aus Kyzikos, ein Schüler des Polemarchos, nach Athen und verbesserte dort den Meton'schen Zyklus. Er fasste vier Perioden des Meton zu einem neuen Zyklus von 76 Jahren mit insgesamt 27759 Tagen zusammen, verkürzte somit die Jahreslänge durch Auslassung eines Tage innerhalb dieser 76 Jahre auf 365 Tage und 6 Stunden. Zwar fand Hipparchos um 125 v. Chr. einen neuen Zyklus von 304 Jahren mit 111035 Tagen, der zu einer noch genaueren Jahreslänge führte. Dieser konnte sich jedoch nicht durchsetzen. Dass das Sonnenjahr 365 ¼ Tage habe, blieb lange ein unerschütterliches Dogma. Ausführlich beschrieben werden die Reformen des Kalenders von Athen bei Ginzel (1914), Bd. II, Seite 378 - 426. (noch lange nicht veraltet)
Der Zyklus des Osterfestes: Die auf dem Konzil von Nikäa 325 beschlossenen rechtlichen Grundlagen zur Feier des Osterfestes wurden von den Patrriarchen in Alexandria in einen praktikablen Kalender umgesetzt. Die dort erarbeiteten Methoden setzten sich im Laufe der Jahrhunderte in der gesamten Christenheit durch. Auch die Reform von 1582 änderte diese Grundlagen nicht. Die Osterrechnung der Alexandriner geht aus von einem neunzehnjährigen Zyklus und einer Jahreslänge von 365 ¼ Tagen. Dass dieser Zyklus nun die nicht ganzzahlige Anzahl von 6939.75 Tagen hat spielt insofern keine Rolle, als in diesem konkreten Fall die Schalttage, je nachdem vier oder fünf pro Zyklus, im Kalender selbst gar nicht auftauchen.
Zurück zur Ausgangsfrage:
Nach Meinung des Verfassers dieser Zeilen sollte man auf keinen Fall in die Osterberechnung einen Zyklus von 76 Jahren einbringen. Dies ist sachlich nicht gerechtfertigt und würde nur den Blick auf die klaren Regeln verstellen. Der neunzehnjährigen luni-solare Zyklus ist im Abendland eng verbunden mit dem Namen Meton. Daher kann man ruhig vom Zyklus des Meton sprechen, auch wenn es sich eigentlich um einen durch die Erkenntnisse des Kallippos verbesserten Meton'schen Zyklus handelt.
Wie dem auch immer sei, die Diskussion Meton oder Kallippos ist rein akademisch. Man sollte nicht glauben, dass die Erkenntnisse dieser Astronomen irgendwelchen Einfluss auf Zeitrechnungen hatten, nicht einmal in ihrer Heimatstadt Athen. Der Rat der Stadt legte weiterhin den Kalender nach eigenem Gutdünken fest. Der alexandrinische Osterzyklus steht darüber hinaus in keinem Zusammenhang mit Zeitrechnungen des antiken oder hellenistischen Griechenland. Er entspringt altjüdischer Tradition, die ihre Wurzeln wiederum in der Zeitrechnung des babylonischen Reiches hatte. Otto Neugebauer hat sicher recht, wenn er schreibt: "It is ridiculous to praise the use of the 19-year cycle for the Easter computus as a survival of the scientific Alexandrian tradition. In fact it is nothing but the return to a simple luni-solar cycle, well known for many centuries."
Am 24. Februar des Jahres 1582 verkündete Papst Gregor XIII. in der Bulle "Inter gravissimas" [zur deutschen Übersetzung] eine Neuordnung des Kalenders, die er auch ausführlich erläuterte. Einer der Grundsätze hierbei war, die alte Ordnung möglichst unangetastet zu lassen. Man wollte lediglich durch geringfügige Änderungen das Datum des Osterfestes wieder in Übereinstimmung bringen mit den Bewegungen von Sonne und Mond. Insbesondere trachtete man, die Bestimmungen des Konzils von Nikäa penibel einzuhalten, in der Hoffnung, dass dann alle Christen der Neuregelung zustimmen könnten. Daher ist in den Quellen auch nie von einer Reformation sondern immer nur von einer Wiederherstellung oder Korrektur des Kalenders die Rede.
Man war damals der in dieser Form nicht ganz zutreffenden Meinung, das Konzil von Nikäa habe 325 folgendes beschlossen:
Der 14. Tag eines Mondmonats ist der Tag des Vollmondes. So wurde volkstümlich die Regel aufgestellt: "Ostern liegt am Sonntag nach dem Frühlingsvollmond."
Im julianischen Kalender ist das Jahr rund 11 Minuten kürzer als der durchschnittliche Zeitraum zwischen zwei Frühlingsäquinoktien. Aus diesem Grund hatte sich in den rund 1250 Jahre seit dem Konzil von Nikäa das astronomische Äquinoktium verschoben und lag nun auf dem 11. März, gegen den 10. März tendierend. Man beschloss nun 1582, 10 Tage aus dem Kalender zu streichen, um so das Äquinoktium auf seinen alten Platz zurückzubringen. Um zu verhindern, dass es sich erneut verschiebe, korrigierte man auch die Schaltregel. Wie bisher sollte jedes vierte Jahr ein Schaltjahr sein. Die "Jahrhundertjahre", also die Jahre 1600, 1700, 1800 etc., sollten jedoch keine Schaltjahre mehr sein, es sei denn, die Jahreszahl liesse sich durch 400 ohne Rest teilen, wie in den Jahren 1600 oder 2000. Diese neue Schaltregel verändert die bisherige Praxis kaum.
Man muss unterscheiden zwischen dem kalendarischen und dem astronomischen Äquinoktium. Der Tag des kalendarischen Äquinoktiums ist, wie vom Konzil 325 festgelegt, der 21. März. Fällt Luna XIV auf den 21. März und ist dieser Tag ein Samstag, so ist Ostern am 22. März, dem frühestmöglichen Termin. Die überkommene Ostergrenze, die man nicht verletzen durfte, ist eingehalten. Das astronomische Fühlingsäquinoktium liegt nach der Neuordnung des Kalenders nun im Zeitraum 19. bis 21. März. Fällt in einen Jahrhundertjahr der Schalttag aus, springt es auf den 21. März, um dann langsam zurückzuweichen bis zum 19. März. Diese kleine Ungenauigkeit gegenüber den Himmelsbewegungen hat man bewusst in Kauf genommen. Wichtiger als übertriebene astronomische Genauigkeit eines Kalenders ist eine einfache Handhabung, die ein jeder nachvollziehen kann.
Hätte man 1582 nicht 10 Tage sondern 11 Tage aus dem Kalender gestrichen, - und dies wurde durchaus diskutiert- , würde das astronomische Äquinoktium in einer Reihe von Jahren auf den 22. März fallen. Dies ist aber auch der früheste Termin für den Ostersonntag. Ostern am Tag des Äquinoktiums zu feiern wäre ein eklatanter Verstoss gegen die wichtigsten Prinzipien der Osterberechnung gewesen. Bereits Kaiser Konstantin, der ja dem Konzil von Nikäa vorstand, hatte 325 in einem Brief an alle Kirchen es als eines der grössten Übel betrachtet, Ostern zweimal im Jahr zu feiern, nämlich einmal nach und dann wieder vor dem Äquinoktium [zum Brief Konstantins in englischer Übersetzung].
Fazit: 1582 musste man genau 10 Tage aus dem Kalender zu streichen. Nur dadurch kam das astronomische Äquinoktium wieder an seine richtige Stelle im Kalender, nämlich auf den 21. März, zum 19. März tendierend. Durch die neuen Schaltregeln wurde dafür gesorgt, dass es auch an dieser Stelle verbleibt. Der gregorianische Kalender wird zu recht in den Quellen als immerwährend (calendarium perpetuum) bezeichnet. Natürlich war es den Gelehrten 1582 klar, dass irgendwann einmal eine erneute Anpassung erfolgen müsse. Dies ändert aber nichts an dem Kalender selbst. Der englische Astronomen John Herschel (1792 - 1871) hat vorgeschlagen, entgegen der bisherigen Regel im Jahr 4000 einen Schalttag einzufügen und dann wieder in jedem Jahr, dessen Jahreszahl durch 4000 ohne Rest teilbar ist. Ob dies sinnvoll ist, wird man in 1500 Jahren wissen. Bis dahin sollte man sich gedulden.
Der greogrianische Kalender ist eine unübertroffene Meisterleistung der Chronologie. Er verbindet klare und einfache Schaltregeln mit einer sehr guten Übereinstimmung mit den Himmelsbewegungen. Leider werden seine Grundzüge bis heute nicht immer verstanden.
| |
|
Seitenanfang | Seitenende |
Der Koran schreibt vor, dass ein Jahr 12 Monate hat und jeder Monat mit jenem Abend beginnt, an dem erstmals nach Neumond die schmale Mondsichel am Abendhimmel sichtbar ist. Somit liegt die Struktur des Kalenders fest. Nichts jedoch wird ausgesagt über die Zählung der Jahre. Rund fünf Jahre nach dem Tod des Propheten einigte man sich darauf, eine eigene islamische Jahreszählung einzuführen und legte fest, dass der Ausgangspunkt das Jahr sein sollte, in dem die Hidschra stattfand. Dies zeigt, welch grosse Bedeutung man diesem Ereignis - dem Abbruch der Beziehungen und Bindungen des Propheten und seiner kleinen Anhängerschar zu seiner Heimatstadt Mekka und seine Übersieldung nach Medina - beimass. Siehe hierzu auch: Die islamische Zeitrechnung
Im julianisch_gregorianischem Kalender hat das Jahr ca. 365 Tage, im islamischen Kalender hingegen nur rund 354 Tage. Daher durchläuft im islamischen Kalender jeder Tag, auch der 1. Muharram, in etwas mehr als 33 Jahren alle Jahreszeiten. Über einen längeren Zeitraum hinweg betrachtet wird der 1. Muharram gleichmässig oft auf jedes Datum im Julianisch/gregorianischen Kalender fallen. Die Wahrscheinlichkeit dafür, dass er auf den 1. Januar fällt, ist also 1 zu 365. Diese statische Zahl sagt allerdings wenig aus über die tatsächliche Verteilung.
Im Islam wird der Monatsbeginn durch Himmelsbeobachtung ermittelt. Bei Umrechnung eines islamischen Datums in den julianisch-gregorianischen Kalender besteht immer eine Unsicherheit von ± 1 Tag. Eine genaue Aussage darüber, in welchen Jahren der Jahresanfang im islamischen Kalender auf den Neujahrstag im julianisch/gregorianischen Kalender fiel, kann daher nicht gemacht werden.
Es gibt auch einen "zyklischen2" islamischen Kalender, der recht genau mit dem Mondlauf übereinstimmt, allerdings von islamischen Theologen durchwegs abgelehnt wird. Zieht man ihn für die Beantwortung der Anfrage heran, kommt man zu folgenden Ergebissen: Der 1. Muharram fiel in folgenden Jahren auf den 1. Januar julianisch: 868, 933, und 1454. Er wäre auch im Jahr 1975 auf den 1. Januar gefallen, aber da war bereits weltweit der gregorianische Kalender eingeführt. Nach dieser 1582 eingeführten gregorianischen Zeitrechnung fällt der 1. Muharram erstmals im Jahre 3084, dann wieder im Jahr 3475 auf den 1. Januar.
Die folgenden Beispiele zeigen, in welchen Jahren nach dem (über die Reform von 1582 hinaus weitergeführten) julianischen Kalender der 1. Muharram auf das angegeben Datum 1. bis 11. Januar fiel. Die Zeitspannen zwischen diesen Jahren werden in der Spalte daneben angezeigt. Auffallend ist, wie häufig dieser Abstand 521 oder 293 Jahre beträgt.
| 1. Januar | 2. Januar | 3. Januar | 4. Januar | 5. Januar | 6. Januar | 7. Januar | 8. Januar | 9. Januar | 10. Januar | 11. Januar | 12. Januar | |||||||||||||||||||||||
| 868 | 640 | 998 | 770 | 835 | 1128 | 900 | 672 | 1030 | 802 | 1095 | 1160 | |||||||||||||||||||||||
| 933 | 65 | 705 | 65 | 1519 | 521 | 1063 | 293 | 1356 | 521 | 1421 | 293 | 965 | 65 | 737 | 65 | 1551 | 521 | 1323 | 521 | 1388 | 293 | |||||||||||||
| 1454 | 521 | 1226 | 521 | 2040 | 521 | 1291 | 228 | 1649 | 293 | 1714 | 293 | 1193 | 228 | 1258 | 521 | 2072 | 521 | 1616 | 293 | 1681 | 293 | |||||||||||||
| 1975 | 521 | 1747 | 521 | 2115 | 75 | 1584 | 293 | 2170 | 521 | 1942 | 228 | 1486 | 293 | 1779 | 521 | 2137 | 65 | 1844 | 228 | 2202 | 521 | |||||||||||||
| 2496 | 521 | 2268 | 521 | 1812 | 228 | 2235 | 293 | 2007 | 521 | 2300 | 521 | 2365 | 228 | 1909 | 65 | |||||||||||||||||||
| 2333 | 65 | 1877 | 65 | 2463 | 228 | 2430 | 521 | |||||||||||||||||||||||||||
| 2398 | 521 | |||||||||||||||||||||||||||||||||
Noch einmal die gleiche Tabelle. Diesmal beziehen sich die Daten auf den (in die Zeit vor der Kalenderreform zurückgerechneten) gregorianischen Kalender.
| 1. Januar | 2. Januar | 3. Januar | 4. Januar | 5. Januar | 6. Januar | 7. Januar | 8. Januar | 9. Januar | 10. Januar | 11. Januar | |||||||||||||||||||||
| 1129 | 738 | 803 | 1031 | 640 | 704 | 1161 | 770 | 835 | 1063 | 672 | |||||||||||||||||||||
| 966 | 228 | 1194 | 391 | 1422 | 391 | 868 | 228 | 933 | 229 | 1324 | 163 | 998 | 228 | 1226 | 391 | 1454 | 391 | 900 | 228 | ||||||||||||
| 1357 | 391 | 1585 | 391 | 1650 | 228 | 1259 | 391 | 1096 | 163 | 1715 | 391 | 1389 | 391 | 1617 | 391 | 1682 | 228 | 1291 | 391 | ||||||||||||
| 1520 | 163 | 1976 | 391 | 1813 | 163 | 1878 | 619 | 1487 | 391 | 2106 | 391 | 1552 | 163 | 2399 | 782 | 1845 | 163 | 2236 | 945 | ||||||||||||
| 1715 | 195 | 2367 | 391 | 2041 | 228 | 2204 | 326 | 1780 | 228 | 2008 | 163 | ||||||||||||||||||||
| 1911 | 196 | 2269 | 65 | 1943 | 163 | 2073 | 65 | ||||||||||||||||||||||||
| 2139 | 228 | 2432 | 163 | 2171 | 228 | ||||||||||||||||||||||||||
| 2302 | 163 | 2334 | 163 | ||||||||||||||||||||||||||||
Das eid ul-fitr, der Tag des Fastenbrechens, fällt auf den 1. Schawwal. Auf die Problematik des Monatsanfangs im islamischen Kalender wird auf dieser Seite mehrfach eingegangen, siehe vor allem den Abschnitt "Der Monatsbeginn im heutigen islamischen Kalender", zur Frage des Neulichts siehe auch: "Der Neue Mond am Abendhimmel". Eine hervorragende Hilfe bei der Frage, ob das Neulicht bereits sichtbar ist, bietet das Programm "Mooncalc" von Dr. Monzur Ahmed, einen entsprechenden Link finden Sie in dem Abschnitt Links und Verweise. Die Frage, wann 1974 der Ramadan endete, ist grundsätzlich nicht eindeutig zu beantworten. Im Iran fiel der 1. Schawwal auf den 17. Oktober, genauer gesagt in die Zeit von Sonnenuntergang des 16. Oktober bis zum Sonnenuntergang des 17. Oktobers. Dies kann abgelesen werden von der Seite "Monatsanfänge im Iran", die hier angegebenen Daten sind historisch belegt. Allerdings war am Abend des 16. Oktober im Iran mit grösster Wahrscheinlichkeit der Mond nicht sichtbar. Auch im Norden Ägyptens und Saudi-Arabiens war das Neulicht wohl nicht sichtbar, dennoch dürften die Kriterien für den Beginn des neuen Monat nach den Kriterien dieser Länder an diesem Tag erfüllt gewesen sein. Dies kann ich allerdings nicht nachprüfen.
Kalender, die auf astronomischen Beobachtungen oder Berechnungen beruhen, haben einen grossen Nachteil: Sind keine weiteren Angaben (wie zum Beispiel der Wochentag) vorhanden, lässt sich ein Datum in der Regel nicht eindeutig bestimmen.
Alle Jahre wieder......
kommt die für den Muslim so wichtige Frage: "Wann ist der Tag des Fastenbrechens?" Die Aussagen des obigen Artikels zum Jahre 1974 gelten natürlich auch für das Jahr 2002.
Dennoch hier einige Daten:
Mittwoch, 4. Dezember 2002
Neumond: Mittwoch, 4. Dezember 2002, 7:37 (UT = mittlere Zeit Greenwich) In einigen Teilen der Welt deutlich sichtbar, da es eine absolute Sonnenfinsternis gab.
Sonnenuntergang in Mekka: 17:38 (Local Time)
Monduntergang in Mekka: 17:48 (Local Time)
Der Mond war an diesem Abend in Mekka mit Sicherheit nicht zu sehen. Wenn überhaupt, war die Mondsichel an diesem Abend in einigen Gebieten nahe des Äquators westlich von Amerika sichtbar.
Donnerstag, 5. Dezember 2002
Sonnenuntergang in Mekka: 17:38 (Local Time)
Monduntergang in Mekka: 18:45 (Local Time)
Der Mond war an diesem Abend in Mekka zu sehen, ebenso in den meisten islamischen Kernländer. Auch in Südeuropa war die Sichel wohl sichtbar, nicht aber in Deutschland.
Daraus folgt: Für die viele Muslime war der 1. Schawwal, der Tag des Fastenbrechens, am Freitag, dem 6. Dezember 2002, beginnend mit dem Sonnenuntergang des Donnerstages. Allerdings folgen nicht alle islamischen Staaten dem Grundsatz, die Mondsichel müsse zumindest theoretisch sichtbar sein.
Da in Saudi Arabien gilt: "Wenn am 29. Tag eines Monats der Monduntergang nach dem Sonnuntergang stattfindet, so beginnt in diesem Moment der neue Monat." (siehe: Der Monatsbeginn im heutigen islamischen Kalender), dürfte in Mekka bereit einen Tag früher das Fasten geendet haben.
In Ägypten gilt, der neue Monat ist angebrochen, wenn zwischen Untergang der Sonne und Untergang des Mondes mindestens fünf Minuten liegen. Am Abend des 4. Dezembers war in Kairo die Differenz zwischen Sonnen- und Monduntergang etwas mehr als neun Minuten, Ägypten feierte daher das Fastenbrechen am 5. Dezember, beginnend mit ebendiesem Mittwoch Abend.
Muslime in Deutschland haben ihre eigene Meinung, wie ein Blick auf ihre homepage http://www.islam.de/ zeigt. Hier die entsprechenden Verlautbarungen des Diwan, des "Deutschen islamwissenschaftlichen Ausschusses der Neumonde":
Noch einmal diese Meldung vom Mittwoch, dem 04.12.2002:
Soeben meldet der "Deutsche islamwissenschaftliche Ausschuss der Neumonde" (DIWAN), der sich am heutigen Tag der Ausschauhaltung in Kerpen traf, dass die Sichtung des Neumondes vom Schawwal erfolgt ist.
Ist dies so gemeint, wie es sich liest, so handelt sich bei dieser Meldung um eine wissenschaftliche Sensation. Wenn am Abend des Mittwochs, des 4. Dezember 2002, in Kerpen das Neulicht gesehen worden ist, so sollte diese Tatsache unverzüglich mit den genauen Daten in naturwissenschaftlichen oder astronomischen Zeitschriften veröffentlicht werden. Alle Arbeiten renommierter Astronomen über das Neulicht wären damit Makulatur.
Der Verfasser bleibt bei seiner Meinung:
Am Abend des 4. 12. 2002 (Mittwoch) war das Neulicht weder in Mekka noch in Kerpen sichtbar.
Am Abend des 5. 12. 2002 (Donnerstag) war das Neulicht in Mekka sichtbar (bei entsprechender Witterung), nicht jedoch in Kerpen.
In einer Reihe von muslimischen Ländern ist die Sichtung des Neulichtes nicht mehr Voraussetzung für das Fastenbrechen, dort feierte man das eid ul-fitr am Donnerstag, dem 5. Dezember 2002. Muslime, die an der alten Vorschrift, dass der Mond sichtbar sein muss, festhalten, feierten einen Tag später.
Diesmal schon im Voraus, ohne danach gefragt worden zu sein, die Stellungnahme zum Ende des Ramadans:
Astronomische Daten:
Neumond, die Konjunktion von Mond und Sonne, ist am Sonntag, dem 23. November 2002 gegen 23.00 Uhr UT.
13 ½ Stunden später, also am 24. November gegen 12.30 Uhr UT, wird der Phasenwinkel des Mondes zur Sonne ca. 8 Grad betragen.
Am Abend des 24. November kurz nach Sonnenuntergang wird voraussichtlich die neue Mondsichel erstmals im südlichen Afrika zu sehen sein, am gleichen Abend dann mit der entsprechenden Zeitverzögerung in Süd- und Mittelamerika. In den USA dürfte die Sichel noch nicht gesehen werden können.
In den zentralen islamischen Ländern wird die Mondsichel am folgenden Abend zu sehen sein.
Muslime, die das Ende des Ramadans von der Sichtung des Neulichts abhängig machen, werden, sofern sie in Südafrika oder in Süd- oder Mittelamerika leben, am Abend des 24. Novembers 2003 das Fasten brechen, der 1. Schawal ist für sie Dienstag, der 25. November. In allen übrigen Ländern, so auch auf der arabischen Halbinsel, in Ägypten, der Türkei, auch in den USA, wird der Zeitpunkt des Fastenbrechens am Abend des 25. Novembers sein, der 1. Schawwal entspricht dann Dienstag, dem 26. November 2003.
Saudi Arabien
Der "Umm al-Qura" Kalender setzt den 1. Schawwal 1424 auf den 25. November 2003. Der Moment des Fastenbrechens in Arabien ist demzufolge am Montag, dem 24. November 2003, nach Sonnenuntergang.
Türkei
In der Türkei wird davon ausgegangen, das die Sichtung des Neumondes erfolgt sei, wenn der Winkelabstand Sonne - Mond grösser als 8 Grad ist. Dieser Augenblick wird Ru'yet (wörtlich Sehen, Sichtung, Einsicht) genannt. Wie oben gesagt ist dies am 24. November gegen 12.30 Uhr UT der Fall, das ist gegen 14.30 Uhr türkischer Winterzeit. In Ankara wird bei Sonnenuntergang der Mond eine Elongation von ca. 9 Grad haben und wird ca. 2 ½ Grad über dem Horizont stehen. Obwohl das zweite Kriterium, das in der Türkei für den Beginn eines neuen Monats erfüllt sein muss, nämlich eine Höhe des Mondes von mehr als 5 Grad über Horizont zur Zeit des Sonnenuntergangs, nicht erreicht wird, wurde für die türkischen Muslime der Abend des 24. November als die Zeit des Fastenbrechens berechnet.
Iran
Im Iran läuft in diesem Jahr der islamische Kalender mit dem zyklischen islamischen Kalender (Epoche 16. Juni) gleich. Dieser Kalender setzt den 1. Schawwal auf den 26. November, daher wird hier am Abend des 25. November nach Sonnenuntergang das Ende der Fastenzeit gekommen sein, also ein Tag später als in den meisten anderen islamischen Ländern.
Resumee
Im Jahr 2003 wir für die meisten Muslime das Fasten im Monat Ramadan enden am Abend des 24. Novembers nach Sonnenuntergang. Nur die Iraner und einige wenige andere Muslime, die nach den alten Vorschriften den Moment abwarten, da die Mondsichel tatsächlich zu sehen ist, werden einen Tag später das Fasten brechen.
geschrieben am Dienstag, dem 28. November 2003
dem 2. Ramadan in der Türkei, dem Iran etc.
dem 3. Ramadan in Saudi Arabien
Nikolaus A. Bär
| |
|
Seitenanfang | Seitenende |
Im April 2018 wurde in der Presse ausführlich über den 70. Jahrestag der Gründung des Staates Israel berichtet. Israel wurde gegründet am 5. Iyar 5708 nach dem jüdischen Kalender, das entspricht dem 14. Mai 1948 nach dem gregorinischen Kalender. Einige Leser kamen offenichtlich mit den angegebenen Kalenderdaten nicht zurecht. Der jüdische Kalender hat so seine Tücken. Er kennt Gemeinjahre zu 12 Monaten und Schaltjahre zu 13 Monaten, wobei eine besondere Schwierigkeit darin liegt, dass der Schaltmonat mitten im Jahr liegt. Der Iyar ist daher mal der 8. und mal der 9. Monat. Der Kalenderrechners arbeitet korrekt, man sollte allerdings die Erläuterungen zu den Kalendertstilen beachten:
5. Iyar 5708 (= 5.9.5708) gleich 14. Mai 1948
5. Iyar 5778 (= 5.8.5778) gleich 20. April 2018
Um Schwierigkeiten bei der Einhaltung der Sabbatregeln möglichst zu vermeiden werden im jüdischen Kalender Feiertage zuweilen verschoben. So kann das Neujahrsfest nur auf einen Samstag, Montag, Dienstag oder Donnerstag fallen. Ausführlich wird dies auf der Seite Der jüdische Kalender erläutert.
Zwischen dem 5. Iyar und dem Neujahrstag des folgenden Jahres liegen immer genau 143 Tage oder 20 Wochen und drei Tage. Daraus folgt, dass der 5. Iyar nur auf einen Freitag, Samstag, Montag oder Mittwoch fallen kann.
Der Staat Israel hat seinen Unabhängigkeitstaqg grundsätzlich auf den 5. Iyar gelegt, jedoch mit folgenden Ausnahmen:
Fällt der 5. Iyar auf einen Montag wird der Unabhängigkeitstag verschoben auf Dienstag 6. Iyar.
Fällt der 5. Iyar auf einen Mittoch wird der Unabhängigkeitstag am gleicen Tag gefeiert.
Fällt der 5. Iyar auf einen Freitag wird der Unabhängigkeitstag verschoben auf Donnerstag 4. Iyar.
Fällt der 5. Iyar auf einen Samstag wird der Unabhängigkeitstag verschoben auf Donnerstag 3. Iyar.
Im Jahr 2018 fiel der 5. Iyar auf Freitag den 20. April. Der Unabhängigkeitstag wurde daher nach der genannten Regel verschoben auf Donnerstag, 19. April. Da im Jüdischen der Kalendertag mit seinem Vorabend beginnt, begann der Unabhängigkeitstag am 18 April 18:00 Uhr Ortszeit (gleich 4. Iyar 5778 0:00 Uhr jüdischer Rechnung).
| |
|
Seitenanfang | Seitenende |
Diese Frage ist nicht so leicht zu beantworten. Es ist unbestritten, dass jede Zeitrechnung, so auch unser julianisch-gregorianische Kalender, beginnt mit dem ersten Tag des ersten Monats des ersten Jahres. Dem ersten Jahr einer Zeitrechnung geht voraus das erste Jahr, dass vor dieser Zeitrechnung liegt. Es gibt keinen "nullten" Tag eines Monats, keinen "nullten" Monat eines Jahres und es kann auch kein "nulltes" Jahr geben.
Diese Regelung ist unbestritten. Allerdings lässt es sich damit nur schwer rechnen. Astronomen benutzen daher eine rein arithmetische Jahreszählung. Dem Jahr 1 geht voraus das Jahr 0, diesem wiederum das Jahr -1. Genauso kennen Astronomen z. B. auch einen 0. Januar. Der 0. Januar 1900 12:00 Uhr ist der Bezugspunkt für die Definition der Ephemeridenzeit, normale Sterbliche würden diesen Zeitpunkt bezeichnen als 31. Dezember 1899 12:00 Uhr.
Heftig diskutiert wurde die Frage, ob es ein Jahr Null gegeben hat, im Zusammenhang mit den Überlegungen, wann ein neues Jahrhundert oder Jahrtausend anfängt. Ein Jahrhundert zählt 100 Jahre. Wenn nun aber das erste (nicht nullte) Jahrhundert beginnen würde mit dem Jahr 1, so würde logischerweise des 2. Jahrhundert mit dem Jahr 101 beginnen, u.s.w. Nun hat allerdings der grosse Wissenschaftler Kaiser Wilhelm II. 1899 angeordnet, dass das der Beginn des 20. Jahrhundert am 1. Januar 1900 gefeiert werden solle. Demzufolge hätte zumindest in Deutschland das 3. Jahrtausend beginnen müssen mit dem Jahre 2000. Ob dieses Gebot des Deutschen Kaisers allerdings heute noch Gültigkeit hat, ist nicht bekannt.
Sicher ist nur eins: Kaiser Wilhelm hatte recht!
Um dies zu beweisen, muss etwas weiter ausgeholt werden. Die heute übliche Jahreszählung geht zurück auf Dionysius Exiguus, einem hochgebildetem Mönch, Mitarbeiter der Kurie in Rom. Im Jahr 525 erhielt er von der Kurie den Auftrag, eine byzantinische Ostertabelle, die Rom zugeschickt worden war, ins Lateinische zu Übersetzen, was er dann auch tat. Allerdings lief diese Tabelle bereits nach sechs Jahren aus, Dionysius schrieb sie um weitere 95 Jahre fort. Das byzantinische Original zählte die Jahre nach der Thronbesteigung Kaiser Diokletians, eine in Byzans übliche Jahreszählung, die Dionysius jedoch nicht übernehmen wollte. Er gab dem ersten Jahr seiner Fortschreibung die Jahreszahl 532 und schrieb dazu, dies sei die Zahlung der Jahre nach der Fleischwerdung (Inkarnation) unseres Herrn, dem Erlöser.
532 Jahre, das ist die Anzahl der Jahre eines grossen Osteryklus, des kleinsten gemeinsamen Vielfachen von 19 (Mondzyklus ) 4 (Schaltjahre) und 7 (Wochentage). Nach 532 Jahren wiederholen sich alle Osterdaten.
Das Jahr 532 in der Zählung nach der Geburt des Herrn ist somit das erste Jahr eines neuen grossen Osterzyklus. Das erste Jahr des 531 endenden Zyklus, das Jahr der Geburt Jesu Christi, ist somit das Jahr, das dem Jahr 1 nach Christi Geburt vorausgeht, wie man es auch immer bezeichnen mag. Die Historiker nennen es das Jahr 1 vor Christus, die Astronomen bezeichnen es als das Jahr 0. Wie dem auch immer sei, da mit diesem Jahr das erste Jahrtausend in der heute allgemein üblichen Jahreszählung nach Dionysius beginnt, beginnt das 3. Jahrtausend am 1. Januar 2000.
Nun ist noch zu begründen, warum Historiker keine Null akzeptieren wollten. Der Grund ist recht einfach: Ihre Quellen sind nahezu alle ursprünglich in Griechisch oder in Latein verfasst. Nun gibt es weder im Griechischen noch im Lateinischen ein Zahlenzeichen für die Null. Wenn dennoch in einer Tabelle oder sonstwo die Zahl 0 vorkam, musste man sie ausschreiben, lateinisch "nulla", griechisch "ουδεν". Claudius Ptolemäus, der wohl bedeuteste Naturwissenschaftler der Spätantike, verfasste seine Werke auf Griechisch. Er war berühmt für seine genauen Positionsbestimmung der Gestirne, und hierzu brauchte er immer wieder auch einmal die Null. Um nun nicht jedesmal "ουδεν" schreiben zu müssen, schrieb er einfach "ο". Nun hat das Omikron zwar den Zahlenwert 70, da aber damals wie heute Sternpositionen im Hexadezimalsystem notiert werden, gab es keine Verwechslungsgefahr. In Rom behalf man sich zuweilen, wenn man nicht immer "nulla" schreiben wollte mit einem Sternchen "∗".
Im altrömischen Kalender begann das Jahr mit dem 1. März. Ungefähr ab dem Jahr 154 vor Christus gab es neben diesem bürgerlichen Jahr noch ein Amtsjahr, beginnend mit dem 1. Januar. Durch die von Gaius Julius Caesar im Jahr 45 vor Christus angeordnete Kalenderreform wurde der Jahresanfang einheitlich auf den 1. Januar festgelegt. Die Römer begingen diesen Tag mit ausgelassenen Festlichkeiten und Ausschreitungen. Diese alte Gewohnheit übernahmen auch die römischen Christen, was der Kirche ein Dorn im Auge war. Sie versuchte mit allen Mitteln gegen dieses "Narrenfest"" vorzugehen.
Im christlichen Kalender gab es unterschiedliche Jahresanfänge (siehe hierzu auch den Eintrag "Stil" im Glossar). Als Tag der Geburt Christi wurde der 25. Dezember angenommen. Acht Tage später, also am 1. Januar, fand die Beschneidung Christi statt (Lukasevangelium 2, 21). Seit Mitte des 6. Jahrhunderts findet sich in den christlichen Festordnungen am 1. Januar das Fest der Beschneidung des Herrn ("Circumcisio domini"). Die Kirche versuchte, durch einen kirchlichen Feiertag dem wilden Treiben an diesem Tag entgegenzutreten, allerdings vorerst ohne grossen Erfolg. Erst ab dem 12. Jahrhundert setzte sich dieser Feiertag allmählich durch. Zu dieser Zeit fand der Jahresbeginn am 1. Januar auch Eingang ins Kirchenrecht, die Kirche liess ihren Festkalender mit diesem Tag beginnen. Diese Entwicklung wirkte sich auch auf das bürgerliche Leben aus. Der 1. Januar als Beginn des Verwaltungs- und Rechnungsjahres fand immer weitere Verbreitung, ab dem 16. Jahrhundert hatte er sich in den meisten abendländischen Staaten durchgesetzt. Ganz verdrängen konnte der Circumcisionsstil die anderen Jahresanfänge bis heute nicht. Die päpstliche Kanzlei datierte bei der Ernennung von Bistümern bis ins 20. Jahrhundert nach dem Annunciationsstil (Jahresanfang am 25. März).
Von Christian Morgenstern stammt das nette Gedicht (»Galgenlieder« 1920), mit dem sich einprägen kann, ob der Mond zu- oder abnimmt. Man muss sich das A und das Z in Kurrentschrift vorstellen:
Als Gott den lieben Mond erschuf,Frage: Stimmt das für Mondbetrachter in Kapstadt, Sidney und auf Feuerland auch? Oder sehen die Bewohner der Südhalbkugel umgekehrt den abnehmenden Mond mit einem Z?
gab er ihm folgenden Beruf:
Beim Zu- sowohl wie beim Abnehmen
sich deutschen Lesern zu bequemen,
ein A formierend und ein Z –
daß keiner groß zu denken hätt'.
Befolgend dies ward der Trabant
ein völlig deutscher Gegenstand.
Auf der südlichen Halbkugel ist alles irgendwie seitenverkehrt. Am einfachsten kann man sich es an einem kleinen Beispiel klarmachen:
Die folgenden Skizzen sollen den Abendhimmel (Blick nach Westen) darstellen, irgendwann zur Zeit der Tag- und Nachtgleiche, einige wenige Tage nach Neumond, kurz nach Sonnenuntergang.
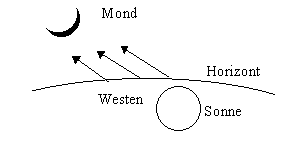 |
Bild 1 zeigt den Blick nach Westen für einen Ort ca. 50° nördlicher Breite. Mittags stand die Sonne genau im Süden, 40° über dem Horizont. Über Südwesten wanderte sie nach Westen und ging dort unter. Sie beleuchtet die vom Betrachter aus gesehen rechte Seite des Mondes. Man könnte die Sichel zu einem Z ausmalen. |
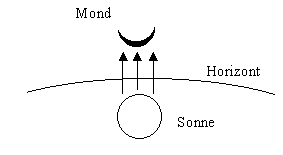 |
Bild 2 zeigt den Blick nach Westen zur gleichen Zeit für einen Ort am Äquator. Mittags stand die Sonne im Zenith. Sie wanderte senkrecht nach Westen und ging dort unter. Sie beleuchtet den Mond von unten. Der Mond sieht aus wie eine Suppenschüssel. |
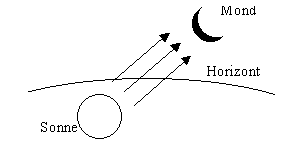 |
Bild 3 zeigt den Blick nach Westen zur gleichen Zeit für einen Ort ca. 50° südlicher Breite. Mittags stand die Sonne genau im Norden, 40° über dem Horizont. Über Nordwesten wanderte sie nach Westen und ging dort unter. Sie beleuchtet die vom Betrachter aus gesehen linke Seite des Mondes. Man könnte die Sichel zu einem A ausmalen. |
Diese Redewendung hat mit dem Kalender nichts zu tun. Um die Frage beantworten zu können muss man einfach in der Bibel nachschlagen und im Evangelium des Matthäus den letzten Satz lesen. Dort steht geschrieben: "Ich bin bei euch alle Tage bis an der Welt Ende". Matthaei am letzten bedeutet also nichts anderes als: "am Ende der Welt" oder: am Ende aller Tage".
| |
Seitenanfang |
| Startseite | Glossar | Gästebuch | Forum | Impressum | FAQ | Inhalt |