| Startseite | Glossar | Gästebuch | Forum | Impressum | FAQ | Inhalt |
| |
|
Seitenanfang | Seitenende |
In Gesellschaften, die einen ausschliesslich am Mondlauf orientierten Kalender benutzen, wird in der Regel der Beginn eines Monats bestimmt durch den Moment, in dem erstmals nach Neumond die schmale Mondsichel wieder am Abendhimmel sichtbar ist. Der Augenschein ist hierbei maßgebend. So war es zur Zeit Christi im jüdischen Kalender und so ist es heute noch im Bereich des Islams. In einigen islamischen Ländern versammeln sich zu Ende des Fastenmonats Ramadan grössere Menschengruppen auf Bergkuppen und beobachten den Horizont im Westen, um dann mit viel Freudengeschrei den Neuen Mond und somit die Zeit des Fastenbrechens zu begrüssen.
Dias erste Erscheinen der jungen Mondsichel am Abendhimmel wird als Neulicht bezeichnet. Der Wunsch, diesen Zeitpunkt im Voraus berechnen zu können, ist verständlich. Schon seit Zeiten der Babylonier und wahrscheinlich sogar schon früher versuchten Astronomen, genaue Kriterien zu bestimmen, die für die Sichtbarkeit des Neulichtes ausschlaggebend sind. Endgültig gelöst ist dieses Problem bis heute nicht.
| |
|
Seitenanfang | Seitenende |
|
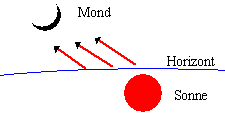
Bei Neumond, also bei Konjunktion von Sonne und Mond gehen beide Gestirne nahezu gleichzeitig auf und unter. Die Sonne bescheint die Rückseite des Mondes, von der Erde aus ist der Mond unsichtbar. Infolge der höheren Bahngeschwindigkeit des Mondes wird der Abstand des Mondes zur Sonne allmählich zunehmen und irgendwann ausreichend gross sein, damit kurz nach Sonnenuntergang die schmale Mondsichel am Himmel für kurze Zeit sichtbar ist. Im Westen wird nun das in der nebenstehenden Skizze angezeigte Bild sichtbar sein.
Damit der neue Mond gesehen werden kann, muss die Mondsichel eine gewisse Breite erreichen, damit sie überhaupt lichtstark genug ist. Ferner muss die Mondsichel noch in einer gewissen Höhe über dem Horizont stehen, sonst würden ihre Strahlen durch die Extinktion ausgelöscht werden. Andererseits muss auch die Sonne tief genug unter dem Horizont stehen, damit sich der Himmel ausreichend verdunkelt.
Der Zeitpunkt des Sonnenuntergangs kann unterschiedlich definiert werden. In der Diskussion über die Sichtbarkeit des Neulichts wird häufig der Moment herangezogen, in dem der Mittelpunkt der Sonne genau im Horizont steht, die Sonnenhöhe also ± 0° beträgt. In diesem Augenblick ist die Sonne natürlich noch voll sichtbar. In der astronomischen Tabellen wird dagegen für den Sonnenuntergang die Zeit angegeben, in der der Sonnenmittelpunkt 0° 50' unterhalb des Horizonts steht. Dies ist der Augenblick, da die letzten Sonnenstrahlen unter dem Horizont verschwinden. Der Halbmesser der Sonne wird dabei berücksichtigt mit ca. 15', die Refraktion mit 35'. Im Englischen wird hierfür meist der Begriff "apparent" oder "visuell" sunset verwendet, während "geometric sunset" den Moment bezeichnet, da der Mittelpunkt der Sonne im Horizont steht. Sofern nicht anderes gesagt, wird bei den folgenden Überlegungen vom "geometric sunset" ausgegangen.
Für den Monduntergang gilt das eben gesagte analog. Allerdings muss hier auch noch die Parallaxe berücksichtigt werden, weshalb für des visuellen Monduntergang eine Höhe des Gestirns von +0° 08' unterstellt wird.
Refraktion: Durch die Erdatmosphäre erfahren eindringende Lichtstrahlen eine Brechung, die zu einer scheinbaren Hebung des Gestirnsortes über dem Horizont führt. Dieses Phänomen wird Refraktion genannt. Ihr genauer Wert ist abhängig von Temperatur und Luftdruck. Bei +10º Temperatur und einem Luftdruck von 760 mm beträgt er für einen Stern genau im Horizont 35' 24''. Steht der Stern 0.5° über dem Horizont, beträgt die Abweichung noch ca. 29', bei einer Höhe von 10° über dem Horizont nur noch ca. 5'.
Extinktion: Der von einem Himmelskörper ausgehender Lichtstrahl wird durch die Erdatmosphäre abgeschwächt. Diese Abschwächung ist umso grösser, je mehr sich der Stern dem Horizont nähert. Eine lichtschwache Mondsichel muss also auch eine gewisse Mindesthöhe über dem Horizont haben, da sonst die Strahlen so stark abgeschwächt werden, das sie gegen die Abendämmerung nicht mehr sichtbar ist
Parallaxe: Unter der Parallaxe des Mondes versteht man die Veränderung des scheinbaren Halbmessers des Mondes je nach seiner Entfernung von der Erde. In Erdnähe beträgt er 16.45', in Erdferne dagegen nur noch 14.73'. Weitere Einzelheiten
Die Verhältnisse am Abendhimmel werden für die kurze Zeit, die für die Sichtbarkeit des Neulichtes eine Rolle spielt, als konstant betrachtet. Streng genommen müsste auch berücksichtigt werden, dass sich der Abstand von Sonne und Mond - gemessen an der Ekliptik - in einer Stunde um mehr als ½ Grad vergrössert.
Um einen Körper im Raum zu beschreiben benötigt man ein Koordinatensystem, das durch einen Nullpunkt, eine Bezugsrichtung und eine Bezugsebene festgelegt ist. In den vorliegenden Ausführungen wurde immer das ekliptikale Bezugssystem verwandt. Bezugsebene ist also die Ekliptik, Bezugsrichtung der Frühlingspunkt. In den astronomischen Jahrbüchern, in denen die Stellung von Sonne und Mond für einen beliebigen Zeitpunkt nachgeschlagen werden kann, werden die Daten teilweise auch nach dem äquatorialen Bezugssystem angeben. Weitere Einzelheiten und Umrechnungsprogramme
Bei den Untersuchung über den Stand von Sonne und Mond am Abendhimmel müsste streng genommen das topozentrische Koordinatensystem Anwendung finden, also der Beobachtungsort zum Nullpunkt des Systems erklärt werden. Dennoch wird gemeinhin mit geozentrischen Daten gearbeitet,der Erdmittelpunkt als Nullpunkt genommen. Beide Systeme unterscheiden sich bei entfernteren Himmelskörpern, wozu in diesem Falle auch die Sonne zu zählen ist, praktisch nicht. Anders verhält es sich jedoch mit dem Mond. Aufgrund seiner Erdnähe sind hier die Differenzen deutlich. Der Mond steht in Wirklichkeit in Horizontnähe ca. 1 Grad tiefer am Horizont als es die Berechnungen nach dem geozentrischen Koordinaten erwarten lassen würden. Astronomen früherer Zeiten betonen daher in der Regel auch immer, dass diese Differenz, die Horizontalparallaxe des Mondes, in die Berechnungen mit einbezogen werden müsste. Anders jedoch bei moderneren Darstellungen. Hier wird in der Regel von geozentrischen Daten ausgegangen, mit der Begründung, da dieser Unterschied im Azimut nur minimal sei und in der Höhe nahezu immer gleich gross, könne man ihn auch weglassen ["I have thought it unneccessary to complicate the calculation by introducing the lunar parallax, because the parallax in altitude is practically constant for any given altitude, while the parallax in azimuth is small, and small changes in azimuth produce no perceptible difference in the result." Fotheringham (1910), Seite 528]. Einzig Yallop berücksichtigt die Parallaxe des Mondes.
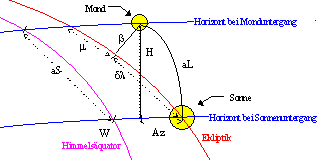
Die folgende Skizze soll die Verhältnisse noch einmal verdeutlichen. Die hier verwendeten Zeichen und Abkürzungen werden im gesamten Text Verwendung finden.
 |
|
Bei den folgenden Überlegungen und Berechnungen wird davon ausgegangen, dass die folgenden Grössen bekannt sind:
Die Bahn, die die Sonne bei ihrem scheinbaren Jahreslauf um die Erde zurücklegt, wird Ekliptik genannt. Diese Ekliptik bildet mit dem Himmelsäquator, dem auf die Himmelskugel projizierten Erdäquator einen Winkel von ca. 23.45°. In einigen islamischen Quellen wird gerundet auch mit 23.50° gerechnet.
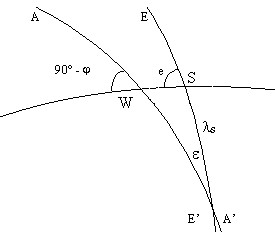
Der Äquator kreuzt die Horizontlinie genau im Westen. Der Winkel, den Horizont und Äquator bilden, ist abhängig von dem Breitengrad des Beobachtungsstandortes. Sein Wert ist 90° - φ.
Der Winkel e zwischen Horizont und Ekliptik im Moment des Sonnenuntergangs ist einerseits abhängig vom Beobachtungsort, andererseits von der Länge der Sonne und somit von der Jahreszeit. Im Frühling, wenn die Sonne im Schnittpunkt von Äquator und der aufsteigenden Ekliptik steht, ist dieser Winkel am grössten (90° - φ + ε), im Herbst am geringsten (90° - φ - ε). Berechnen lässt er sich am einfachsten über zwei Hilfswinkel x und y.
 |
|
||||||||||||||||||||||||||||
Weit verbreitet war und ist der Versuch, anhand des Mondalters das Neulichtes vorherzusagen. Die Faustregel lautet: Sind bei Sonnenuntergang mehr als 24 Stunden verflossen, so ist die Mondsichel sichtbar. So einfach diese Regel auch ist, so unsicher ist sie auch
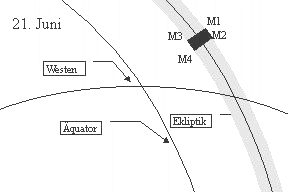
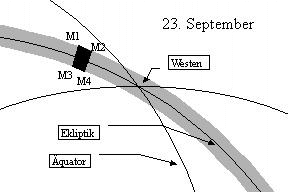
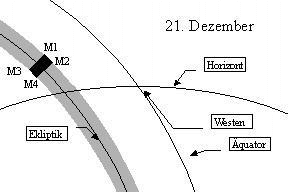
Wieviel Zeit seit der Konjunktion von Sonne und Mond verflossen sein muss, damit diese beiden Gestirne am Abendhimmel ausreichend weit voneinander entfernt sind, hängt zum einen ab von der Neigung der Ekliptik gegen den Horizont, also von der Lage des Beobachtungsortes und der Jahreszeit, zum anderen von der Bahngeschwindigkeit des Mondes und seinem Abstand zur Ekliptik. Zu Frühlingsbeginn steht die Ekliptik steil am Abendhimmel, der Mond wird sehr schnell einen grossen Abstand von der Sonne in der Höhe gewinnen, während die Differenz Sonne - Mond im Azimut klein bleiben wird. Umgekehrt sind die Verhältnisse bei Beginn des Herbstes. Sonne und Mond werden einen grösseren Abstand im Azimut haben, während der Abstand in der Höhe nur langsam zunehmen wird. Die folgenden Skizzen sollen diesen Sachverhalt verdeutlichen. Auch die Bahngeschwindigkeit des Mondes ist sehr unterschiedlich. Steht der Mond im Perigäum, also in Erdnähe, wird er seine grösste Geschwindigkeit erreichen und in 24 Stunden mehr als 15 Grad in der Ekliptik zurücklegen. Steht er dagegen in Erdferne, so legt er am Tag weniger als 12 Grad zurück.
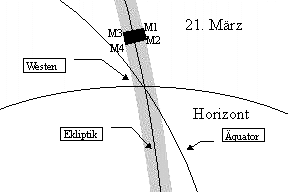
Bei gleichem Mondalter können also am Abendhimmel sehr verschiedene Verhältnisse auftreten:
 |
 |
|
| Frühling | Sommer | |
 |
 |
|
| Herbst | Winter |
Es bedeutet:
| M1 | Mond im Perigäum Abstand Sonne - Mond (δλ): 15.5° Grösste nördliche Breite (β = 5.3°) |
M2 | Mond im Apogäum Abstand Sonne - Mond (δλ): 11.75° Grösste nördliche Breite (β = 5.3°) |
|
| M3 | Mond im Perigäum Abstand Sonne - Mond (δλ): 15.5° Grösste südliche Breite (β = - 5.3°) |
M4 | Mond im Apogäum Abstand Sonne - Mond (δλ): 11.75° Grösste südliche Breite (β = - 5.3°) |
Rechenprogramm und Beispieltabelle
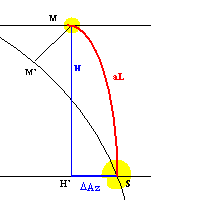
Der Abstand von Sonne und Mond in Höhe bei Sonnenuntergang wurde zu einem wichtigen Kriterium bei der Frage der Sichtbarkeit des Neulichtes.
 |
|
Der Abstand Sonne - Mond lässt sich wie folgt berechnen:
sin aD = sin H = sin e cos β sin Δλ + cos e sin β
Es gilt ferner: cos aL = cos aD * cos ΔAz
In der englischsprachigen Literatur wird der Unterschied zwischen Sonne und Mond in der Höhe als arc of descent (aD) bezeichnet, wobei dann noch unterschieden werden kann zwischen der Höhe des Mondes über Horizont (h) bei einer bestimmten Depression der Sonne (s), also aD = h + s.
zum allgemeinen Rechenprogramm
Zusätzlich zum vertikalen Abstand von Sonne und Mond muss auch der azimutale Abstand der beiden Himmelskörper berücksichtigt werden. Dieser im Horizont gemessene Abstand ΔAz ist immer positiv, unabhängig davon, ob der Mond bei Sonnenuntergang nördlich oder südlich von der Sonne stand: ΔAz = | ΔAz |.
Er berechnet sich folgendermassen:
tan ΔAz = cos e tan Δλ - sin e tan β / cos Δλ
Auf eine weitere Möglichkeit, diese letztgenannten beiden Grössen zu bestimmen, wird im folgenden Absatz über den arc of light eingegangen.
zum allgemeinen Rechenprogramm
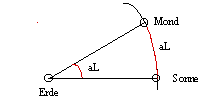
| Der arc of light ist der direkte Bogenabstand Sonne Mond. Er ist gleichzeitig der Winkel Sonne - Mond - Erde. Er läßt sich wie folgt berechnen: cos aL = cos β cos Δλ |
 |
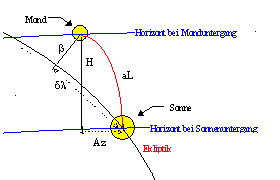 |
Ist der arc of light bekannt, so kann mit seiner Hilfe die Höhe des Mondes über Horizont (H) sowie der azimutale Abstand (Az) berechnet werden. Der Winkel, den aL mit dem Horizont bildet, ist die Summe der Winkel e (Neigung der Ekliptik) und γ (Hilfswinkel).
| Es gilt nun: |
sin γ = sin β / sin aL; tan γ = tan β / sin Δλ sin H = sin aL sin (e + γ) tan Az = cos(e + γ) tan aL |
zum allgemeinen Rechenprogramm
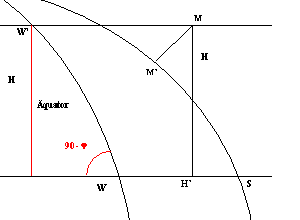
Als arc of separation (aS) wird jenes Bogenstück des Äquators bezeichnet, das begrenzt wird durch den Horizont bei Sonnenuntergang und den Horizont bei Monduntergang. Seine Grösse ist zugleich ein Zeitmass, da der Himmelsäquator in 24 Stunden einmal den Westpunkt durchläuft. 1 Grad entsprechen 4 Zeitminuten. Er spielte vor allen in früheren Zeiten eine grosse Rolle bei der Beurteilung der Wahrscheinlichkeit, die junge Mondsichel sehen zu können.
 |
|
Ist die nördliche Breite des Beobachtungsortes und die Höhe des Mondes über dem Horizont bei Sonnenuntergang bekannt, lässt sich der Arc of separation leicht berechnen:
| Es gilt: | sin aS = sin H * cos φ |
zum allgemeinen Rechenprogramm
Der arc of vision ( arcus visionis, Sehungsbogen) ist astronomisch definiert als der senkrechte Abstand der Sonne (nach Sonnenuntergang) zum Horizont zur Zeit des Auf- oder Untergang eines Sternes. Er entspricht also der Depression der Sonne im genannten Augenblick. Dieser Winkel spielt vor allem bei der Definition von Dämmerungserscheinungen oder bei der Frage, ob ein Stern in der Dämmerung bereits gesehen werden kann, ein grosse Bedeutung.
Im Zusammenhang mit der Bestimmung des Neulichtes entspricht er der Depression der Sonne s bei Untergang des Mondes.
Da bei der Diskussion der Sichtbarkeit des Neulichts der Abstand Sonne zu Mond in der Höhe in der Zeit zwischen Sonnenuntergang und Monduntergang als gleichbleibend angenommen wird gilt vereinfachend folgende Gleichsetzung:
arc of vision = arc of descent = H = h + s.
zum allgemeinen Rechenprogramm
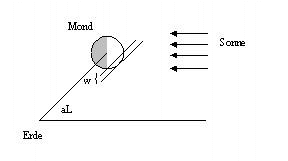
Der scheinbare Durchmesser des Mondes schwankt - von der Erde aus gesehen - je nach der Entfernung von Erde und Mond. Er beträgt im Schnitt rund 30 Bogenminuten. Kurz nach Neumond ist natürlich nur ein kleiner Teil des Mondes, eben jene schmale Mondsichel, zu sehen. Der Durchmesser des dicksten Teils dieser Sichel in der Mitte zwischen den beiden Spitzen sei als Weite des Mondes[ 3 ] bezeichnet. Sein Wert ist in erster Linie abhängig vom arc of light.
 |
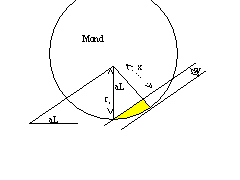 |
Die Weite (w) lässt sich leicht berechnen:
| d ist der Durchmesser des Mondes. Er schwankt je nach Entfernung des Mondes zwischen 32.9' und 29.5' d/2 = r; w = r - x; cos aL = x/r w = d/2 (1 - cos aL) w = d sin² (aL / 2) |
zum allgemeinen Rechenprogramm
Die obigen Ausführungen über die Weite der Mondsichel würden gelten für eine ideal glatte Mondoberfläche. Nun ist aber der Mond voller hoher Gebirge und tiefer Krater. Kurz nach Neumond werden von der Erde aus gesehen - vereinfacht gesagt - nur die Bergspitzen von hinten beleuchtet, die Täler liegen noch tief im Schatten. Von der Mondsichel ist daher nur ein Teil dessen sichtbar, was bei einer glatten Oberfläche zu sehen sein müsste. Die Sichel ist an einigen Stellen unterbrochen, sie ist kaum grösser als 90°. Wird der beleuchtete Teil des Mondes grösser, so kehrt sich dieser Effekt um. Nun ist nicht nur jener Bereich erkennbar, der bei einer glatten Oberfläche sichtbar sein müsste sondern darüber hinaus auch noch die Spitzen der benachbarten Gebirge. Der arc of deficiency beschreibt das Mass dieses Effektes.
Der Franzose André Danjon (1890 - 1967), ehemaliger Direktor des Observatoriums von Strassburg, untersuchte dieses Phänomen genauer. Er zeigte, dass bei einem Winkelabstand Sonne zu Mond von mehr als 40 Grad der deficiency arc negativ ist, also der sichtbare Teil des Mondes grösser ist als bei einer glatten Oberfläche. Für Werte unter 40 Grad nimmt der deficiency arc jedoch stetig zu und erreicht bei einem Winkelabstand von 7 Grad ebenfalls 7 Grad. Das heisst, ab dieser Grenze ist die Mondsichel auf keinen Fall mehr sichtbar. Daraus darf aber nicht gefolgert werden, dass bei einem grösseren arc of light der Mond immer sichtbar sein muss. Eine weiter Folgerung ist, dass bei Neumond der Mond immer für geraume Zeit unsichtbar bleibt, da selbst bei grösstmöglicher Breite des Mondes der Winkelabstand nie mehr als 5½ Grad betragen kann.
Das "Danjon Kriterium" gilt inzwischen als widerlegt. Technische Hilfsmittel ermöglichten auch Sichtungen bei einer Elongation von weniger als sieben Grad.
| |
|
Seitenanfang | Seitenende |
Seit es Kalender gibt, die auf dem Mondlauf basieren, und seitdem Astronomen die Bahnen von Sonne und Mond vorherberechnen können, seit ältesten Zeiten also wurde versucht, den Moment im Voraus zu bestimmen, an dem zum ersten Mal nach der Konjunktion der neue Mond am Abendhimmel zu sehen ist.
Die Babylonier waren sicher nicht die ersten, die hierfür Regeln aufstellten, sie sind aber die ersten, von denen sie überliefert sind. Sie präzisierten die alte Vorstellung, nach der bei Sonnenuntergang mindestens ein Tag seit der Konjunktion vergangen sein musste und stellten jenes Kriterium auf, das bis in die jüngste Zeit nahezu uneingeschränkt gültig blieb:
Das Neulicht kann dann gesehen werden, wenn der arc of separation grösser oder gleich 12 Grad ist, d. h. wenn zwischen Sonnenuntergang und Monduntergang mindesten 48 Minuten liegen.
Zu Ende des sechsten Jahrhunderts nach Christus entwickelte sich in Indien ein Hochblüte der Naturwissenschaften. Zu den bekanntesten Abhandlungen über Astronomie dieser Epoche gehören neben dem Pancha Siddhantikdas das Surya Siddhanta. In diesen Werken wird auch ausführlich auf die Frage des Neulichts eingegangen. Eine der astronomischen Fragestellung angepasste Übersetzung der entsprechenden Stelle des Surya Siddhanta findet sich bei Bruin (1977). Die Inder gingen von den gleichen Bedingung für die Sichtung der Mondsichel aus wie die Babylonier,
Die frühen islamischen Astronomen griffen unstreitig auf diese indischen Quellen zurück. Bald gingen sie jedoch ihre eigenen Wege und waren über viele Jahrhunderte hinweg in der Astronomie und in der Chronologie führend.
An erster Stelle ist hier wohl der in Bagdad lehrende Mathematiker und Astronom al Khorazmi (um 860) zu nennen, der auch im Abendland wohl bekannt war und ist, stand doch sein Name Pate für das Kunstwort Algorithmus. 30 Jahre später entstand das Werk al Battanis, dessen Passagen über das Neulicht ebenfalls von Bruin (1977) ins Englische übertragen wurden. Weiter Werke folgten, die genaue Anweisungen zur Berechnung des Standes von Sonne und Mondes enthielten. Häufig waren Tabellen beigefügt, aus denen man, differenziert für einzelne Breitengrade, die Daten ablesen konnte.
Erwähnt werden muss in diesem Zusammenhang auch der Jude Maimonides, der sich ebenfalls ausführlich mit dem Neulicht und der Sanktionierung des Monatbeginns im jüdischen Kalender befasst hat.
Ein neuer Ansatz kam dann in der Mitte des 19. Jahrhunderts aus dem Westen. Das vertiefte Beschäftigung mit Fragen des Mondkalenders und des Neulichtes war sicherlich hervorgerufen durch das Interesse an Astronomie und Kalender der altorientalischen Völker und auch durch den Versuch, den alten jüdischen Kalender zu rekonstruieren, um das Todesdatum Jesu Christi bestimmen zu können.
Der Astronom Julius Schmidt beschäftigte sich intensiv mit diesen Fragen und sammelte in den Jahren 1850 - 1867 während eines Aufenthaltes in Griechenland zahlreiche (positive und negative) Neu- und Altlichtbeobachtungen. 1910 veröffentlichte Fotheringham eine grundlegende Arbeit. Unter Zuhilfenahme der Aufzeichnungen von Schmidt sowie weiterer Astronomen und Laien berechnete er für jede dieser Beobachtungen die Differenz von Sonne und Mond in Höhe und Azimut am Abendhimmel. Er stelle fest, dass sich hierdurch eine klare Grenzlinie ergibt für die Sichtbarkeit der Mondsichel. Die Differenz in der Höhe müsse mindestens 12 Grad betragen, bei grösserem Abstand im Azimut könne auch ein geringerer Unterschied in der Höhe ausreichen.
Ein Jahr später antwortete Maunder auf diese Arbeit. Er bestätigte zwar grundsätzlich die Thesen von Fotheringham, wies aber zurecht darauf hin, dass dieser seine Grenzlinie an den negativen Beobachtungen ausrichtete, nicht an den positiven. Dass der Mond nicht sichtbar gewesen sei, sei jedoch von nicht so grosser Beweiskraft wie ein offensichtlich erkennbares Neulicht. Demzufolge zog Maunder die Grenzlinie etwas tiefer. Der Indian Ephemeris and Nautical Almanac benutzt die gleichen Kriterien, zieht allerdings die Grenzlinie noch etwas tiefer.
Carl (auch: Karl) Schoch, der 1924 bis 1926 eng mit Fotheringham zusammengearbeitet hatte (vgl. den Nachruf von P. V. Neugebauer in: Astronomische Nachrichten, Bd. 237 (1930), S. 221 - 224) veröffentlichte im Jahre 1927 seine "Planetentafeln für Jedermann". Sie enthalten eine kleine Tabelle mit Kriterien für die Sichtbarkeit des Neulichtes, die, wie Schoch selbst schreibt, denen von Maunder sehr nahe kommen [Schoch 1927, S. 14]. Kurze Zeit später überarbeitete er diese Tabelle. Im Jahr 1930 gab P. V. Neugebauer im Selbstverlag publizierte Schriften aus dem Nachlass von Schoch heraus. Hier sind auch diese Berichtigungen abgedruckt. [Schoch 1930, S. B 17]. Aus in seiner 1929 erschienenen Astonomischen Chronologie bringt Neugebauer die verbesserte Tafel Schochs [Neugebauer 1929, Bd. II, Tafel E 21].
Δ bezeichnet den Abstand Sonne Mond im Azimit
h die Höhe des Mondes über Horizont bei Sonnenuntergang
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Seit dem Jahre 1966 werden in den "Indian Ephemeris and Nautical Almanacs" Neulichttabellen abgedruckt. Diese Jahrbücher konnten nicht eingesehen werden, die dort verzeichneten Werte werden jedoch häufig zitiert [z. B. Ashbrook 1971, S. 79]. Diese Indian Epheremis stimmen mit der verbesserten Tabelle Schochs überein.
Vergleich der Kriterien von Fotheringham, Maunder, Schoch und den Indian Ephemeris
| Differenz in Azimut |
Mindesthöhe des Mondes | ||||
| Fotheringham | Maunder | Schoch (1927) | Schoch (1930) | Indian Ephemeris | |
| 0 | 12.0 | 11.0 | 10.7 | 10.4 | 10.4 |
| 5 | 11.9 | 10.5 | 10.3 | 10.0 | 10.0 |
| 10 | 11.4 | 9.5 | 9.6 | 9.3 | 9.3 |
| 15 | 11.0 | 8.0 | 7.6 | 8.0 | 8.0 |
| 20 | 10.0 | 6.0 | 6.2 | 6.2 | |
| 23 | 7.7 | (4.8) | |||
Einen ganz neuen Weg geht Frans Bruin. Er konstatiert zuerst, dass die Helligkeit des Abendhimmels nahezu gleich ist für alle Punkte x, y, für die in Bezug auf den Punkt des Sonnenuntergangs gilt: -30°< x <+30° und: +1°< y <+20°. Sie ist in diesem Bereich auschliesslich davon abhängig, wie tief die Sonne unter dem Horizont steht. Als nächstes berücksichtigt er die Extinktion, die Abschwächung der Lichtstrahlen durch die Erdatmosphäre, die sich in Horizontnähe besonders stark bemerkbar macht. Dabei bezieht er sich auf eine Tabelle, aus der hervorgeht, bis zu welcher Höhe ein Himmelskörper bestimmter Helligkeit trotz Extinktion noch sichtbar sein kann. Nun berechnet er anhand einer Veröffentlichung von Siedentopf, welche Helligkeit ein Himmelskörper von gegebener Grösse haben muss, um vor einem Hintergrund mit gegebener Helligkeit noch sichtbar zu sein. Er geht dabei davon aus, dass die Gestalt des Himmelskörpers keine Rolle spiele, dass also eine Mondsichel mit z. B. einer Weite von 0.5 Bogenminuten gleichzusetzen sei einer Scheibe mit diesem Durchmesser.
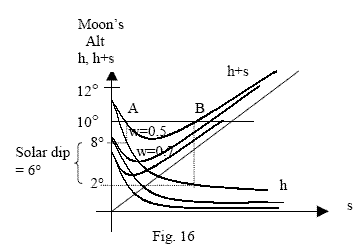
|
| Grafik aus Leong Wen Xin (1999) |
Anhand all dieser Kriterien entwickelt er nun eine Grafik, die es nicht nur gestattet, zu erkennen, ob das Neulicht überhaupt sichtbar ist, sondern aus der auch mit einer Genauigkeit von 5 Zeitminuten abgelesen werden kann, für welchen Zeitraum die Mondsichel am Himmel sichtbar ist. Bekannt sein muss lediglich die Weite des Mondes (w), die unabhängig ist vom Beobachtungsort und die Höhe des Mondes über Horizont bei Sonnenuntergang (H bzw. aD) am Beobachtungsort. Die erste Kurve in Bruins Grafik gilt füe eine Weite der Sichel von 0.5 Bogenminuten. Ist z. B. der arc of Descent (aD = H = h + s) gleich 10°, so ist eine Gerade zu ziehen, die die y-Achse bei 10° schneidet. Sie schneidet die Kurve fü w = 0.5' in den Punkten A und B. Die Sichel wird erstmals sichtbar werden an Punkt A. Die Sonne steht dann knapp 2° unter Horizont. Ist Punkt B erreicht, wird der Mond wieder unsichtbar werden, die Sonne steht dann ca 8° unter Horizont. Am tiefsten Punkt der Kurve, bei einer Depression der Sonne von ca. 4.2°, wird der Moment der besten Sichtbarkeit erreicht sein. Es ist also mit Hilfe der Grafik auch möglich, den Zeitpunkt der besten Sichtbarkeit zu bestimmen. Steht der Mond bei Sonnenuntergang 9° über Horizont, wird die entsprechende Gerade die Sichtbarkeitskurve nur streifen. Der Mond wird also nur für einen kurzen Moment sichtbar sein bei einer Höhe von 4° über Horizont und einer Depression der Sonne von 5°.
Bruin gibt nur eine grafische Lösung, keine rechnerische.
Kritiker der Arbeit Bruins haben darauf hingewiesen, dass das Neulicht schon viel früher, auch bei einer Sichelweite von 0.25' oder weniger, sichtbar sein kann.
1997 ging Bernard D. Yallop noch einen Schritt weiter. In einer als "Technical Note" des Nautical Almanac Office 1998 veröffentlichten Arbeit versucht er, die Ansätze von Frans Bruin mit den Kriterien von Munder und Schoch (= Indian Ephemeris) zu verbinden. Er ist der Meinung, die von Bruin ermittelten Mindestbedingungen für die Sichtbarkeit der Sichel seien bei einem grösseren Abstand von Sonne und Mond im Azimuth ungenügend, sie würden das Neulicht in höheren Breitengraden häufig zu spät ansetzen. Daher greift er für seine Berechnungen auf die Werte der Indian Ephemeris zurück, übernimmt aber von Bruin sowohl den Zeitpunkt der bestmöglichen Sichtbarkeit des Mondes wie auch die Weite der Mondsichel als Kriterium, wober er auch die Parallaxe des Mondes berücksichtigt.
| Weite der Mondsichel | ||
| nach Bruin: | SD = 15.0 w = SD * (1 - cos aL) | |
| nach Yallop: | SD = 0.27245 * π SD' = SD * (1 + sin h * sin π) w' = SD' * (1 - cos aL) = SD' * (1 - cos H * cos ΔAz) wobei h die geozentrische Höhe und π die Parallaxe des Mondes ist. |
|
Den Moment der bestmöglichen Sichtbarkeit der Mondsichel betrachtet Yalopp nach Bruin als gegeben, wenn die Sonne den 5/9 Teil der Höhendifferenz von Sonne und Mond unter Horizont steht.
Wenn: aD = H = h + s , dann ist der beste Zeitpunkt bei: s = H / 9 * 5 und h = H / 9 * 4
Damit die Sichel sichtbar ist, muss die Höhe H des Mondes nach den Indian Epheremis bei Sonnenuntergang folgende Bedingung erfüllen:
H > 10.3743 - 0.0137 * ΔAz - 0.0097 * ΔAz * ΔAz
Yallop führt nun den Parameter q ein, der den Grenzwert beschreibt:
q = H - (10.3743 - 0.0137 * ΔAz - 0.0097 * ΔAz * ΔAz)
Ist q > 1 werden die Kriterien der Sichtbarkeit erfüllt, ist q = 0, ist der Grenzwert erreicht.
Nun ersetzt Yallop in der obigen Formel ΔAz durch w
q = H - 11.8371 - (6.3226 * w + 0.7319 * w * w - 0.1018 * w * w * w) q = q / 10
Dieser Parameter q ermöglicht es nun, die Differenz des Mondes zur Grenzlinie zu bestimmen und so genauere Kriterien für die Sichtbarkeit oder Nicht-Sichtbarkeit des Neulichtes aufzustellen.
| (A) | q > | +0.216 | leicht sichtbar | |
| (B) | +0.216 | ≥ q > | -0.014 | sichtbar unter perfekten Bedingungen |
| (B) | -0.014 | ≥ q > | -0.160 | sichtbar, ggf. mit optischen Hilfsmittel |
| (B) | -0.160 | ≥ q > | -0.232 | sichtbar, optische Hilfsmittel notwendig |
| (B) | -0.232 | ≥ q > | -0.293 | auch mit Fernrohr nicht sichtbar |
| (B) | -0.293 | ≥ q | nicht sichtbar, da unter dem Danjon Kriterium |
Die Methode Yallop wird heute weithin als die genaueste Möglichkeit betrachtet, die theoretische Sichtbarkeit einer frühen Mondsichel zu erkunden.
| |
|
Seitenanfang | Seitenende |
Die Frage, welche Bedingungen gegeben sein müssen, damit nach Neumond die schmale Mondsichel am Abendhimmel wieder sichtbar ist, beschäftigt die Menschheit seit Jahrtausenden. Eine eindeutige Antwort konnte darauf bis heute nicht gegeben werden, und so ist diese Diskussion bis heute nicht verstummt, im Gegenteil, sie hat in den letzten Jahrzehnten an Heftigkeit eher zugenommen.
Vor hundert Jahren gab es nur einige wenige Spezialisten, die sich mit dem Neulicht beschäftigten. Bei Ausgrabungen vor allem im Nahen und Mittlerem Orient hatte man sehr viel Material gefunden. Naturwissenschaftler und Geisteswissenschaftler suchten gemeinsam, die Astronomie und Chronologie dieser Kulturen zu erforschen. Umfassende Tabellenwerke entstanden, mit deren Hilfe die unglaubliche Genauigkeit der gefundenen Angaben über Finsternisse, über den Aufgang und den Untergang von Sternen und über andere Ereignisse aufgezeigt werden konnte. Auch der heliakische Untergang des Mondes, das Neulicht eben, spielte hierbei eine Rolle.
Dies stiess auf allgemeines Interesse, und so wurde die Zahl von Laien, die sich auf die Jagd nach einem möglichst jungen Mond machten immer grösser. Heute sind es vor allem Amateurastronomen, die mit Hilfe moderner Techniken zum Teil wunderbare Ergebnisse vorlegen.
Auch von muslimischer Seite ist in den letzen Jahrzehnten ein verstärktes Interesse an den Fragen des Neulichts festzustellen. Der islamische Kalender ist heute der einzige, der allein durch den Mondlauf gelenkt wird und bei dem der Monatsbeginn vom Augenschein abhängt, wie im Koran festgelegt. Dort steht das Wort Hilal (pl. ahilla), das sich ableitet von erscheinen, sich neu zeigen , das also genau dem Ausdruck Neulicht entspricht. Muslimische Autoritäten scheinen dabei immer wieder zu neuen Ergebnissen zu kommen, denn einige islamische Länder haben in der letzten Zeit ihren Kalender mehrfach geändert. Derzeit wird auch heftig diskutiert, welche technischen Hilfsmittel angewendet werden dürfen.
Über all dem sollte aber nicht vergessen werden, dass es letztendlich nur um eine klare Interpretation von Koran, Sure 2, Vers 189 geht:
"Man fragt dich nach den Neulichten (ahilla). Sag: Sie sind (von Gott gesetzt als) feste Zeiten für die Menschen, und für die Wallfahrt."
| |
|
Seitenanfang | Seitenende |
| |
Seitenanfang |
| Startseite | Glossar | Gästebuch | Forum | Impressum | FAQ | Inhalt |