Seitenanfang

Seitenende

Bruin ging in der Neulichtfrage neue Wege. Sein Vorgehen soll hier ausführlicher dargestellt werden:

1.:
Sind die Ephemeriden von Sonne und Mond bekannt, kann man daraus den arc of light berechnen. Siehe: Rechenprogramm

2.:
Ist der arc of light al bekannt, kann man daraus die Weite der Mondsichel w berechnen.
Ist die Weite der Mondsichel w bekannt, kann man daraus den arc of light aL berechnen
Es besteht ein eineindeutiger Zusammenhang zwischen aL und w.

Relation von Weite der Mondsichel w zum arc of light aL:

      Der Halbmesser des Mondes ist bei Bruin immer 15'
      scheinbarer Radius des Mondes = r = 15

      w = r * (1 - cos aL)
      w / r = 1 - cos aL
      cos aL + w/r = 1
      cos aL = 1 - w / r

         al     w               w        aL
         8     0.15             0,15     8.11
        10     0.23             0.30    11.48
        12     0.33             0,50    14.84
        14     0.45             0.70    17.75
        16     0.58             0.90    19.95
        18     0.73             1.00    21.04
        20     0.90             1.25    23.56
        22     1.09             1.50    25.84
        24     1.30             1.75    27.95
        26     1.52             2.00    29.93
        28     1.76             2.50    33.56
        30     2.01             3.00    36.87

3.:
Ist der arc of light aL (oder die Weite der Mondsichel w) bekannt und die Höhe H des Mondes bei Sonnenuntergang, kann daraus der Abstand Sonne Mond im Azimut ΔAz berechnet werden

    cos aL = cos H * cos ΔAz
    cos ΔAz =  cos aL / cos H
    cos H = cos aL / cos ΔAz
  

Berechnung von ΔAz bei und gegebenen aL oder w für die Höhe 10°

    aD = H = 10°

        al   w aus aL  H     Az           w      aL aus w   H     Az

        10     0.23    10    0.00
        12     0.33    10    6.47         0.30    11.48     10    5.41
        14     0.45    10    9.71         0,50    14.84     10   10.89
        16     0.58    10   12.45         0.70    17.75     10   14.43
        18     0.73    10   14.96         0.90    19.95     10   17.28
        20     0.90    10   17.34         1.00    21.04     10   18.54
        22     1.09    10   19.63         1.25    23.56     10   21.38
        24     1.30    10   21.87         1.50    25.84     10   23.90
        26     1.52    10   24.07         1.75    27.95     10   26.19
        28     1.76    10   26.24         2.00    29.93     10   28.31
        30     2.01    10   28.39         2.50    33.56     10   32.64

Berechnung von ΔAz bei gegeben Höhe H und gegebenen aL oder w

    w sei:       0.5'             w sei:        1.0'
    aL ist dann 14.84°            aL ist dann: 21.04°


         w     H      Az         w     H         Az

        0.5  14.84     0.0       1.0   21.04     0.0
        0.5  14        5.0       1.0   20        6.6
        0.5  12        8.8       1.0   18       11.1
        0.5  10       11.0       1.0   16       13.8
        0.5   8       12.5       1.0   14       15.7
        0.5   6       13.6       1.0   12       17.4
        0.5   4       14.3       1.0   10       18.6
        0.5   2       14.7       1.0    8       19.5
        0.5   1       14.8       1.0    6       20.2
        0.5   0       14.8       1.0    4       20.7
                                 1.0    2       20.9
                                 1.0    0       21.04

4.:
Bruin ermittelt nun die Mindesthöhe über Horizont, die eine Mondsichel von einer bestimmten Weite haben muss aus:

• der Helligkeit des Abendhimmels als Folge der Depression der Sonne. Hierbei geht er davon aus, dass einem Bereich von +- 30° im Azimut und von +1° bis +20°in der Höhe, bezogen auf den Ort des Sonnenuntergangs, ist die Helligkeit des Himmels gleich.
• dem notwendigem Kontrast zwischen Sichel und Hintergrund. Er greift auf eine Untersuchung von Siedentopf zurück. Dieser führte 1940 Versuche durch in denen er ermittelte, wie gross der Kontrast zwischen einer kleinen runde Fläche und der Umgebungshelligkeit sein muss, damit der kleine Kreis noch erkannt werden kann. Vor einem dunklem Hintergrund ist ein heller Punkt leicht zu erkennen. Je heller nun der Hintergrund wird, je geringer also der Kontrast in der Helligkeit zwischen Objekt und Hintergrund ist, desto schwieriger ist der Punkt zu erkennen, irgendwann ist er nicht mehr vom Hintergrund zu unterscheiden. Siedentopf führte die Versuche mit Punkten verschiedener Grössen durch [Siedentopf]. Seine Ergebnisse wertete er in logarithmischen Kurven aus.
• des Einflusses der Extinktion.

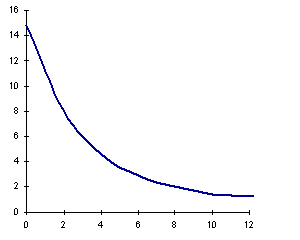
Das nebenstehende Diagramm zeigt das Ergebnis dieses Berechnungen Bruins für eine Sichel mit Weite w = 0.5': h zu s für w = 0.5' s h 2 7.8 4 4.4 6 3.0 8 2.0 Steht die Sonne z. B. 4° unter Horizont, muss die Sichel 4.6° oder höher über dem Horizont stehen, damit sie gesehen werden kann.

5.:

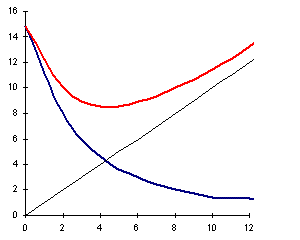
In einem weiteren Schritt setzt Bruin die obige Kurve nun gegen den Wert (h + s), biegt sie also um 45°. Dies ist dann die endgültige Kurve der Sichtbarkeit des Neulichts bei einer Weite der Sichel v0n 0.3' Steht z. B. am Beobachtungsort der Mond bei Sonnenuntergang 10° über dem Horizont aD = 10°), lege man eine Gerade durch h = 10 (grüne Linie). Diese Linie schneide die Kurve der Sichtbarkeit an zwei Punkten. Die Sichel wird erstmalig sichtbar sein bei einer Depression der Sonne von 2° und verschwindet wieder bei einer Depression von 8.4°. Die bestmögliche Sichtbarkeit ist erreicht am Tiefpunkt der Kurve, wenn die Sonne 4° unter Horizont steht.

Bruin zeigt keine Möglichkeiten zur Berechnung des Neulichts auf. Er gibt lediglich eine graphische Lösung des Problems.

Seitenanfang

© 2001 - 2006 Nikolaus A. Bär    zur E-mail Adresse