| Startseite | Glossar | Gästebuch | Forum | Impressum | FAQ | Inhalt |
| N A. B | Kannte Beda die Null? |
| Gliederung | |
| Vor einiger Zeit wurde im Internet eine Diskussion über die Frage geführt, ob Beda die Null kannte. Auch die Seite http://www.nabkal.de wurde dabei einmal zitiert, obwohl es zu diesem Thema bisher hier kaum etwas zu finden war. Dies soll nun nachgeholt werden. | |
| |
|
Seitenanfang | Seitenende |
Um auf die Titelfrage antworten zu können muss man erst einmal auf die Darstellung der Zahlen allgemein und besonders auf die Darstellung der Null eingehen.
Die ursprünglichste Art, Zahlen zu notieren, vom Verfasser noch häufig angewandt, ist sicher folgende: Man mache für die 1 einen Strich, für die 2 zwei Striche und so fort. Mehr als vier Striche kann der Mensch nicht auf einmal erfassen, er müsste anfangen zu zählen. Daher mache man bei der 5 einen Querstrich und hat somit ein eigenes Zeichen geschaffen. Alle alten Zahlensysteme, von wenigen exotischen Ausnahmen abgesehen, beruhen auf diesem Prinzip. Die Zahlen sind in Fünfer- und Zehnergruppen geordnet. Dies hat wohl seine einfache Ursache darin, dass der Mensch zehn Finger hat. Das Zählen mit den Fingern ist die einfachste Rechenmethode, bis heute in Gebrauch.
Gut unterrichtet sind wir über Zahlen- und Schriftzeichen aus den mesapotamischen Kulturen. Dort hatte man schon sehr früh eine wichtige Entdeckung gemacht, um dauerhaft etwas zu notieren zu können. Man trug in einem Beutel einen Klumpen feuchten Lehms mit sich. Wollte man etwas aufschreiben, nahm man sich ein Stück, formte daraus eine Tafel und ritzte seine Notizen mit einem Griffel oder Stift ein. Legte man den Ton dann in die Sonne wurde er steinhart. Eine Vielzahl solcher Tontafeln sind erhalten geblieben.
Die alten babylonischen Ziffern sahen ungefähr folgendermassen aus:
| 1 | 5 | |||||
| 2 | 10 | |||||
| 3 | 20 | |||||
| 4 | 30 | u.s.w. |
Es handelt sich hier um ein additives Zahlensystem, das heisst, der Wert einer Zahl ergibt sich aus der Addition der einzelnen Ziffern. Eine Zeichen für die Null braucht man in einem derartigen System nicht. Auch als das Ergebnis von Berechnungen war die Null als Zahl unbekannt. Wenn in einer Kornkammer 4 Säcke Getreide liegen und man nimmt diese 4 Säcke weg, was ist dann das Ergebnis? Nun, die Kornkammer ist leer. Auch heute würde niemand sagen: "Die Zahl der Getreidesäcke ist gleich Null." Oder: Wenn man von der Zahl 20 die Zahl 20 abzieht, was ist dann das Ergebnis? Nun, Sie wissen es. Dies beiden Beispiele sind übrigens nicht neu erfunden, sie finden sich auf Keilschrifttexten aus Susa (Ifrah, S. 423).
Mit einem derartigen Zahlensystem lässt es sich allerdings nur sehr schwer rechnen, wie am Beispiel der römischen Zahlen noch einmal aufgezeigt werden wird. Wohl erstmalig zu Beginn des 2. Jahrtausends vor Christus taucht bei den Babyloniern ein Stellenwertsystem auf. Wie bei dem heutigen Dezimalsystem war nicht mehr nur der Wert einer Ziffer von Bedeutung sondern auch die Stellung der Ziffern in der Zahl. Basis dieses System war die Zahl 60.
Mit dem Hexagesimalsystem kann man auch sehr grosse und sehr kleine Zahlen recht kompakt schreiben:
Die dezimale Zahl 662706,21 entspricht hexagesimal 3; 4; 5; 6: 12; 36
| 603 | 602 | 601 | 600 | 60-1 | 60-2 | entspricht 648000 + 14400 + 300 + 6 + 0,2 + 0,01 |
| 3 | 4 | 5 | 6 | 12 | 36 |
Da nun die Stellung der Ziffern innerhalb einer Zahl von Bedeutung ist, taucht das Problem auf, wie man leere Stellen kennzeichnen kann. In einer Tafel aus dem 2. Drittel des 2. Jahrtausend vor Christus heisst es: Das Quadrat der Zahl: 2; 27 ist: 6; 9. Ein Zwischenraum zwischen der 6 und der 9 ist nicht zu erkennen. Man sieht auf den ersten Blick, das dies nicht stimmen kann. Das Quadrat von 2; 27 [147 dezimal] ist natürlich 6; 0; 9 [21609 dezimal].
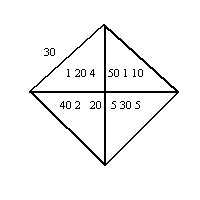
| Als weiteres Beispiel sei ein Tonscherben aus dem 18. Jahrhundert vor Christus angeführt. Man sieht ein auf der Spitze stehendes Quadrat mit den beiden Diagonalen. Am linken Rand steht dreimal das Zeichen für 10, zu lesen als 0: 30 gleich 0,5 dezimal. Im Quadrat stehen zwei Zahlen. Die obere ist zu lesen 1: 24; 51; 10 gleich 1,414212963 dezimal Die untere ist zu lesen 0: 42; 25; 35 gleich 0,707106481 dezimal Der Sachverhalt ist eindeutig: In einem Quadrat mit der Seitenlänge 1 ist der Wert der Diagonale 1,414212963, der halbe Wert - daher die Zahl 0,5 am Rande - ist 0,707106481. Die modernen Werte: Wurzel 2: 1,414213562 ½ Wurzel 2: 0,707106781 |
 |
Wie man sieht musste man schon ein guter Mathematiker sein, um Zahlen in Keilschrifttexten richtig zu interpretieren, wobei das grösste Problem die fehlende Null war. So mag es verwundern, dass man erst zu Beginn des 4. Jahrhunderts vor Christus begann, Leerstellen in Zahlen zu kennzeichnen . Man verwendete hierzu Zeichen, die etwa so ![]() oder
oder ![]() aussahen. Nun war es möglich, sogar zwei oder mehr leere Stellen in einer Zahl eindeutig darzustellen.
aussahen. Nun war es möglich, sogar zwei oder mehr leere Stellen in einer Zahl eindeutig darzustellen.
Wenn man so will, waren diese Zeichen die erste Null in der Weltgeschichte.
| 1 | α | 10 | ι | 100 | ρ | 1000 | 'α | ||||
| 2 | β | 20 | κ | 200 | ς | 2000 | 'β | ||||
| 3 | γ | 30 | λ | 300 | τ | 3000 | 'γ | ||||
| 4 | δ | 40 | μ | 400 | υ | 4000 | 'δ | ||||
| 5 | ε | 50 | ν | 500 | φ | 5000 | 'ε | ||||
| 6 | ς | 60 | ξ | 600 | χ | 6000 | 'ς | ||||
| 7 | ζ | 70 | ο | 700 | ψ | 7000 | 'ζ | ||||
| 8 | η | 80 | π | 800 | ω | 8000 | 'η | ||||
| 9 | θ | 90 | ϙ | 900 | ↑ | 9000 | 'θ |
Die Griechen benutzten die Buchstaben des Alphabets als Zahlenzeichen. Gross- und Kleinbuchstaben wurden unterschiedslos verwendet, ein Zeichen für die Null gab es nicht. Gegenüber den Keilschriftziffern stellten diese Buchstabenzahlen einen grossen Fortschrift dar. Dreimal das Zeichen für Zehn nebeneinander geschrieben konnte in Mesopotamien sowohl 30 wie auch 620 oder 4356610 bedeuten, gegebenenfalls auch 0,5 Die griechischen Ziffern waren hingegen eindeutig.
Im antiken Griechenland war das Schreiben auf Tontäfelchen unbekannt. Für Notizen benutzte man mit Mehl bestäubte Brettchen oder kleine Sandkästen, in die man seine Kreise zeichnete. Lediglich Inschriften, Münzen und einige wenige auf Pergament oder Papyrus geschrieben Werke überdauerten die Jahrhunderte. In ihnen sind vor allem natürliche Zahlen verzeichnet, bei denen sich das Problem mit der fehlenden Null nicht stellt.
Im wissenschaftlichen Bereich gebrauchten die Griechen gleich den Babyloniern das Hexagesimasystem, allerdings nur für die Darstellung von Brüchen. Hier trat nun wieder die Frage auf, wie fehlende Stellen gekennzeichnet werden können. Einer der grössten Astronomen war der um 160 nach Chr. in Alexandria verstorbene Ptolemäus, bekannt besonders für seine äusserst genauen Bestimmungen von Gestirnsörtern. Dieser errechnete z. B. für den Stand der Sonne in einem bestimmten Moment den folgenden Wert:
| ηλίου | α' | β' | γ' | δ' | ε' | ς' | |
| σς | νθ | ο | ις | ιγ | μη | λ | |
| ° Sonne | i | ii | iii | iv | v | vi | |
| 206 | 59 | 0 | 16 | 13 | 48 | 30 | |
| Dies entspricht ca. 206,98340851 Grad | |||||||
Die Sonne hat in diesem Beispiel eine Länge von 206 Grad, 59 Minuten, keine Sekunden, 16 Terzen u.s.w. Im griechischen Test findet sich bei den Sekunden ein Zeichen, das nahezu aussieht wie eine moderne Null. Es ist aber nicht anderes als ein Omikron. Zwar hat das Omikron den Zahlenwert 70, eine Siebzig kann es aber in einem hexagesimalen System nicht geben, eine Verwechslungsgefahr besteht also nicht. Vielmehr steht es hier als Abkürzung für griechisch ουδεν, lateinisch nullum, deutsch nichts.
Die römischen (lateinischen) Zahlen dürften allgemein bekannt sein:
| 1 | I | 5 | V | 500 | D | |||
| 2 | II | 10 | X | 1000 | M | |||
| 3 | III | 50 | L | |||||
| 4 | IIII | 100 | C |
Ein Zeichen für die Null gab es nicht,
Diese römischen Zahlen entwickelten sich ähnlich wie die meisten frühen Systeme wie oben gezeigt aus einer einfachen Aneinanderreihung von Einzelzeichen ähnlich wie bei den Keilschriftziffern. Die Eins war ein Strich, mehrere Striche wurden zusammengefasst, und so entstanden besondere Zeichen für Fünf und Zehn, dann auch für 50, 100, 500, und 1000. In einer späteren Stufe wurden diese Ziffern durch ähnlich aussehende Buchstaben ersetzt.
Die Zahlen sind somit älter als die Schriftzeichen. Erst in späterer Zeit wurden sie der Schrift angepasst. Das Zeichen M für Tausend ist somit keineswegs eine Abkürzung von "mille". Vielmehr dürfte die Entwicklung ungefähr folgendermassen verlaufen sein:
| Aus ursprünglich: | wurde | dann | und schliesslich |
Bei diesen "additiven" Zahlensystemen spielt es keine Rolle, an welcher Stelle ein Zahlenzeichen steht. Die einzelnen Werte werden einfach zusammengezählt. Rechnen kann man damit nur schwer:
| Beispiel | |
| CCCXIII | |
| + | CCCXIII |
| + | MLXVII |
| + | DCLXXX |
| = | MMLX |
Aus diesem Grund empfiehlt Beda übrigens den Gebrauch der griechischenn Zahlen.
| |
|
Seitenanfang | Seitenende |
Nun zurück zur Ausgangsfrage: Kannte Beda die Null? Je nachdem, wie man diese Frage interpretiert, kann es darauf zwei Antworten geben.
Mit seinem umfangreichem Werk über die Zeitrechnung wollte Beda den Ostertabellen und den damit zusammenhängenden Rechengrundlagen des Dionysius Exiguus zum Durchbruch verhelfen, was ihm letztendlich auch gelang. Beda zitiert Dionysius immer wieder, teilweise wortwörtlich. Das "Liber de paschate" des Dionysius und Bedas "De Temporum Ratione" sind untrennbar miteinander verbunden.
Die christliche Osterberechnung beruht auf einem Zusammenspiel des Mondjahres und des Sonnenjahres. Ein Mondjahr ist 11 Tage kürzer als ein Sonnenjahr. Beginnen also Sonnen und Mondjahr irgendwann einmal am gleichen Tag, so wird im folgenden Jahr zwischen dem Beginn des Mondjahres und dem Anfang des Sonnenjahres eine Differenz von 11 Tagen sein, ein Jahr später wird der Unterschied 22 Tage betragen, im dritten Jahr dann 33 Tage. In diesem Fall wird im Mondjahr ein zusätzliche Monat von 30 Tagen eingeschoben, der Unterschied zwischen beiden Jahreformen reduziert sich auf drei Tage. Nach 19 Jahren fällt der Beginn des Mondjahres und des Sonnenjahres wieder zusammen. Diese Zusatztage, die man dem Anfang des Mondjahres hinzufügen muss, um auf den Beginn des Sonnenjahres zu gelangen, werden griechisch ημέραι επάκται, lateinisch epactae oder dies adiectiones (von griechisch επ-αγειν, lateinisch adiicere "hinzufügen") genannt. Sie sind die wichtigsten Osterkennzeichen.
Im letzten Jahr eines 19jährigen Zyklus gibt es 18 Epakten oder "dies adiectiones". In diesem Fall muss man am folgenden Jahresbeginn 12 Tage hinzufügen, gelangt also auf 30 Epakten. Dies entspricht einem vollen Mondmonat, den man in Abzug zu bringen hat. Zieht man von 30 Epakten diese 30 Tage ab, so bleiben "keine Epakten", lateinisch "nullae epactae" oder im Singular "nulla epacta".
Propter quod idem ultimus epactas, id est adiectiones lunares XVIII tunc retinens, primo anno non XI, ut in caeteris annis fieri solet, sed XII dies accommodat. Et quia XXX dierum fine volvuntur, nulla epacta in principio ipsius cycli ponuntur. Beda, DTR, cap 42
Anno primo (circuli decemnovennalis), quia non habet epactas lunares, pro eo quod cum noni decimi inferioris anni XVIII, et suis XI epactis, addito etiam ab Aegyptiis die una, fiunt XXX, id est luna mensis unius integra, et nihil remanet de epactis, et quod in Aprili mense incidit eo anno luna paschalis XIV, tene regulares in eo semper XXXV, subtrahe XXX, id est ipsa luna integra, et remanent V. Dionysius, Argumentum XIV
In den Listen, in denen für jedes Jahr das Datum des Ostersonntags sowie die wichtigsten Jahreskennzeichen verzeichnet sind, steht in der Spalte der der Epkten in diesen Jahren "nulla", "nulla epacta" oder "nullae epactae"
Hier ein Auszug aus dem "Liber de paschate" des Dionysius Exiguus:
ANNI DO- QVAE EPC- CON- QVO- QUOTA DIES DOMI- LUNA
MINI SINT CTAE CUR- TUS SIT LVNA NICAE FE- IPSIUS
NOSTRI INDI- I.E. REN- SIT XIII PA- STIVITATIS DIEI
IESV TIO- ADIE- TES LVNAE SCHALIS DOMI-
CHRISTI NES CTIO- DIES CIR- NICI
NES CVLUS
LVNA-
RES
B DXXXII X NULLA IIII XVII NON.APR. III ID. PR. XX
DXXXIII XI XI V XVIII VIII KAL.APR. VI KAL. APR. XVI
DXXXIIII XII XXII VI XVIIII ID.APR. XVI KAL.MAI. XVII
DXXXV XIII III VII I IIII NON.APR. VI ID.APR. XX
B DXXXVI XIIII XIIII II II XI KAL.APR. X KAL.APR. XV
DXXXVII XV XXV III III IIII ID.APR. II ID.APR. XVI
DXXXVIII I VI IIII IIII III KAL.APR. II NON.APR. XVIIII
DXXXVIIII II XVII V V XIIII KAL.MAI. VIII KAL.MAI. XX OGD.
B DXL III XXVIII VII VI VII ID.APR. VI ID.APR. XV
DXLI IIII VIIII I VII VI KAL.APR. II KAL.APR. XVIII
DXLII V XX II VIII XVII AKL.MAI. XII KAL.MAI. XVIIII.
DXLIII VI I III VIIII II NON.APR. NON.APR. XV
B DXLIIII VII XII V X VIIII KAL.APR. VI KAL.APR. XVII
DXLV VIII XXIII VI XI II ID.APR. XVI KAL.MAI. XVIII
DXLVI VIIII IIII VII XII KAL.APR. VI ID.APR. XXI
DXLVII X XV I XIII XII KAL.APR. VIIII KAL.APR. XVII
B DXLVIII XI XXVI III XIIII V ID.APR. II ID.APR. XVII
DXLVIIII XII VII IIII XV IIII KAL.APR. II NON.APR. XX
DL XIII XVIII V XVI XV KAL.APR. VIII KAL.MAI. XXI END.
DLI XIIII NULLA VI XVII NON.APR. V ID.APR. XVIII
B DLII XV XI I XVIII VIII KAL.APR. II KAL.APR. XX
Beliebt waren im Mittelalter Tabellen zur Bestimmung des Osterdatums, die häufig nur eine einzige Seite umfassten, und in denen die Osterkennzeichen für jedes beliebige Jahr abgelesen werden konnten. In so einem Tabellenfeld war natürlich nicht ausreichend Platz für "nulla" oder gar "nulla epacta". Dieses Feld einfach leer zu lassen verbot sich aus den oben genannten Gründen. Da es nun aber im Lateinischen kein Zeichen für "nullum" gab, beholf man sich zumeist damit, dass man ein * setzte. Zuweilen findet sich auch die Zahl XXX. Zwar kann es keine Epakte XXX geben, jeder aber, der mit derartigen Tabellen umzugehen verstand, wusste dies.
Es gibt eine Vielzahl weiterer Jahreskennzeichen. Dionysius Exiguus bringt im Anschluss an seine Osterlisten noch einige Argumenta paschalia, Rechenregeln, mit deren Hilfe man diese Jahreskennzeichen bestimmen kann. Beda geht auf sie in den entsprechenden Kapiteln des Liber de Temporum Ratione ebenfalls ein. Sie unterliegen gewissen Zyklen. Um sie zu berechnen, muss man daher eine Division durchführen, bei der nur der ganzzahlige Rest von Bedeutung ist (eine Modulo-Division).
Beispiel: Berechnung der Indiktion, einem Zyklus von 15 Jahren, der der Absicherung der Jahreszahl diente. Die Berechnung ist recht einfach: man addiere zu der Zahl der Jahre 3, teile die so gewonnene Summe durch 15. Der verbleibende ganzzahlige Rest ist die Indiktion. Bleibt kein Rest (ist der Rest gleich Null), sie ist die Konkurrente 15.
Si vero nihil remanserit, XV indictio est. [Dionysius, Argumentum II]
Si vero nihil remanserit, decima quinta est. [Beda DTR,l cap. IL ]
Allgemein gilt nach Dionysius: Wenn es keinen Rest gibt (wenn der Rest gleich Null ist), so ist als Rest der Divisor zu nehmen:
Ne tibi forsitan aliqua caligo erroris occurrat, per omnem conputum, per quem ducis, si nihil superfuerit, eundem conpotum esse, per quem ducis, agnosce, ut puta, si per X et VIIII ducens nihil superfuerit, XVIIII esse, si per XV, quindecimum, et si per VII, septimum. Argumenta paschalia, arg. VIII
Fazit: Aus all dem geht klar hervor: Beda kannte "nullum" oder "nihil" als Ergebnis von Berechnungen. Gleiches gilt für seinen "Vorgänger" in Fragen der Osterberechnung Dionysius Exiguus. Dieser wiederum hatte die Ostertabellen der Ägypter, das heisst der Alexandriner, fortgeschrieben und deren Rechenvorschriften übernommen. Von Alexandria aus lässt sich die Spur weiter zurückverfolgen bis in die graue Vorzeit. Seit Jahrtausenden konnte man mit "nullum" oder "nihil" rechnen, unabhängig davon, ob man dafür ein Zeichen hatte oder nicht.
Natürlich kannte Beda die Null nicht, jedenfalls dann nicht, wenn darunter die von den indischen Ziffern abgeleitete Zahl "0" verstanden wird.
Entstanden ist das indische Zahlensystem im 5. bis 6. nachchristlichen Jahrhundert in Nordindien. Ein vom 28. August 458 datierter in Sanskrit geschriebener Text enthält bereits ein vollständig ausgearbeitetes dezimales Positionssystem mit einer Null. Die erste dezimale Zahlschrift mit identischem Aufbau wie die modernen Ziffern findet sich in einer Schenkungsurkunde aus Kupfer aus dem Jahre 595 [Ifrah, S. 550 - 551]. Die Kunde von diesen neuartigen Ziffern verbreitete sich rasch. Mitte des 7. Jahrhunderts verfasste der syrische Bischof Severus Sebokt in einem Kloster in dem (damals bereits islamisch beherrschten) Mesopotamien eine Schrift, in der es u. a. heisst: "Ich werde hier nicht von den Wissenschaften der Hindu reden, nicht von ihren subtilen Entdeckungen in der Astronomie,.... ich möchte nur von den Rechnungen sprechen, die mit neun Ziffern vollzogen werden." [Ifrah, S. 490]
Es dauerte aber noch 3 Jahrhunderte, bis diese Ziffern in den christlichen Westen gelangten. Zuerst tauchten sie im Zusammenhang mit Rechenbrettern auf. Diese Tafeln waren schon im alten Rom in Gebrauch. Auf einem Brett wurden Spalten aufgezeichnet, jeweils für die Einer, die Zehner, die Hunderter u.s.w. Anfangs rechnete man mit kleinen Steinchen, den "calculi". Waren in einer Spalte 10 oder mehr Steinchen, nahm man 10 "calculi" weg und setzte dafür ein Steinchen in die nächst höhere Spalte. Im 10. Jahrhundert wurde dieses Verfahren stark vereinfacht indem man anstelle von Steinchen kleine Hornplättchen, sogenannte "apices" verwendete. Auf diesen Plättchen waren Zahlen geschrieben, entweder mit römischen oder griechischen Zeichen, zunehmend dann mit den indischen Ziffern. Auch bei diesem System brauchte man noch keine Null. Mit diesem Rechenbrettern konnte man multiplizieren und dividieren, ohne dass die Kenntnis der Null überhaupt nötig gewesen wäre. [Ifrah, S. 532]
Erst ab der Wende des 11. zum 12. Jahrhunderts finden sich die indischen Ziffern dann auch in Handschriften. Die beginnende Renaissance hatte einen enormen Aufschwung der Wissenschaften gebracht, der nicht zuletzt islamisch-arabischer Einflusses zu verdanken war. In der Mathematik waren es vor allem die Werke des um 850 verstorbenen Ibn Musa al Chorazmi über die Algebra und die Arithmetik, die wesentlich dazu beitrugen, diese nunmehr "arabisch" genannten Zahlen im Abendland bekannt zu machen. Das von seinem Beinamen "der Chorazmier" abgeleitete Wort Al-gorithmus wurde als Bezeichnung für das dezimale Positionssystem indischen Ursprungs und die damit verbundenen Rechenregeln gebraucht. Erst hiermit war die Null in der heutigen Bedeutung in die abendländische Mathematik eingeführt.
Wenn es auch zu Lebzeiten Bedas bereits im Osten Gebiete gab, in denen das indisch-arabische Ziffernsystem bekannt war, Beda selbst kannte es nicht, Zumindest gibt es in den hier genau durchsuchten beiden Werken über die Zeitrechnung keine einzige Stelle, die in diese Richtung hin umgedeutet werden kann.
Die Schriften Bedas liegen in gedruckter Form vor und sind in wohl jeder wissenschaftlichen Bibliothek Deutschlands einsehbar. Wer behauptet, Beda habe die Ziffer "Null" im Sinne der heute gebräuchlichen Zahlen gekannt, möge dies bitte mit genauer Quellenangabe belegen.
| |
|
Seitenanfang | Seitenende |
Beda Venerabilis: De Temporum Ratione
Beda Venerabilis: De Temporibus
Dionysius Exiguus: Liber de Paschate
Dionysius Exiguus: Argumenta paschalia
Görke, Winfried: Die Null und der Computer - über historische Wurzeln der Technischen Informatik
Claudius Ptolemäus: Syntaxis Mathematica
Ifrah, Georges: Universalgeschichte der Zahlen, Frankfurt/New York 1991
| |
Seitenanfang |
| Startseite | Glossar | Gästebuch | Forum | Impressum | FAQ | Inhalt |