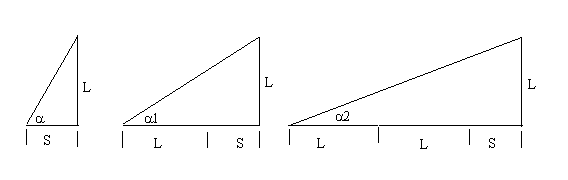| N A. B |
Astronomische Zeitbestimmung im Islam
Astronomische Berechnung der Zeiten
|
| Gliederung |
|
Astronomische Zeitbestimmung im Islam
II Die Berechnung der Zeiten
Die Verhältnisse am Himmel
Um die Stellung der Gestirne am Himmel bestimmen und ihre Bewegungen berechnen zu können, braucht man ein Bezugssystem. Auf- und Untergangszeiten von Himmelskörpern sind abhängig vom Standort des Beobachters. Daher kann der Bezugspunkt nur der Beobachtungsort sein. Bezugsebene ist die vom Horizont begrenzte Ebene, in deren Mittelpunkt der Bezugsort liegt. Über der Horizontebene wölbt sich der sichtbare Teil der Himmelskugel, unter ihr der für den Beobachter unsichtbare Teil.
Die Verhältnisse am Himmel soll die unten folgende Skizze verdeutlichen. Der Punkt direkt über dem Standort des Beobachters, der "höchste" Punkt des Himmels, wird Zenit (Z) genannt. In einem mehr oder weniger grossen Abstand hiervon befindet sich der Himmelspol (P), der Punkt, an dem die verlängerte Erdachse den Himmel erreichen würde. Um diese Achse scheint sich die Himmelskugel mit ihren Sternen einmal pro Tag um 360 Grad zu drehen. Der Himmelspol befindet sich senkrecht über dem Mittelpunkt der Ebene, die durch den Himmelsäquator (A A') begrenzt wird. Der Himmelsäquator ist der auf die Himmelskugel projizierte Erdäquator. Der Abstand von Pol zu Zenit hängt ab von der geographischen Breite (φ) des Beobachtungsortes. Am Nordpol fallen Pol und Zenit zusammen, am Äquator liegt der Himmelspol im Horizont. Allgemein gilt: Bogen PZ = 90° - φ. Der direkte Abstand eines Himmelskörpers, in diesem Fall der Sonne (S), zum Äquator wird Deklination (δ) genannt. Der Abstand der Sonne zum Horizont ist d die Höhe über (oder auch unter)dem Horizont. Sie wird hier mit h bezeichnet.
Die Sonne dreht sich auf ihrer Kreisbahn DD' in 24 Stunden einmal um den Pol P. Der Winkel ZPS gibt somit die Zeitdifferenz zwischen aktuellem Sonnenstand und dem Durchgang durch den Zentralmeridian wieder. Er wird daher Stundenwinkel /τ) genannt. Der Winkel SZP gibt die Himmelsrichtung an, in der die Sonne steht.
Die Verhältnisse am Himmel sollen durch die folgende Skizze verdeutlicht werden:
Die Sonne dreht sich auf ihrer täglichen Kreisbahn DD' in 24 Stunden um den Pol P. Der Winkel Z P S gibt somit die Zeitdifferenz zwischen dem aktuellen Sonnenstand und dem Durchgang durch den Zentralmeridian wieder. Er wird daher auch Stundenwinkel τ genannt. Der Winkel SZP ist der Azimuthwinkel. Er gibt die Himmelsrichtung an, in der die Sonne steht. Der Winkel bei S ist kaum von praktischer Bedeutung.
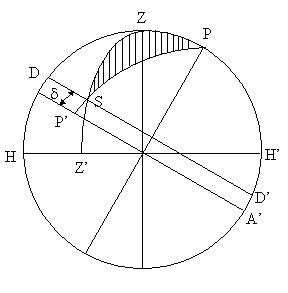
|
| Z: | Zenit |
| P: | Pol |
| S: | Sonne (oder Gestirn) |
| H Z P H': | Zentralmeridian |
| H H': | Horizont |
| A A': | Himmelsäquator |
| D D': | Bahn der Sonne (am gewählten Tag) |
| S P' = D A: | δ Deklination der Sonne |
| S Z': | h Höhe der Sonne über/unter Horizont |
| A Z: | φ Geographische Breite |
| P Z: | 90 - φ (Abstand (Zenit - Pol ) |
| P S: | 90 - δ (Abstand (Sonne - Pol |
| Z S: | 90 - h (Abstand (Sonne - Zenit) |
| Winkel Z P S: | τ Stundenwinkel |
| Winkel S Z P: | Azimutwinkel |
|
Dieses Dreieck, gebildet aus dem Pol, dem Zenit sowie der Sonne oder einem Stern spielt nicht nur in der Astronomie sondern auch in der Nautik eine grosse Rolle. Es wird daher auch nautisches Dreieck genannt.
Bestimmung der Deklination
Die Bahn, die die Sonne auf ihrer jährlichen Bahn um die Erde am Himmel beschreibt, wird als Ekliptik bezeichnet. Unterteilt wird sie zumeist in 360 Grad oder in 24 Stunden. 15 Grad entsprechen einer Stunde. Der Abstand der Sonne vom Frühlingspunkt (0 Grad) ist die ekliptikale Länge der Sonne. Mit dem Himmelsäquator, den auf die Himmelskugel verlängerten Erdäquator, bildet die Ekliptik einen Winkel von etwa 23.45 Grad, hier mit ε bezeichnet. In islamischen Quellen finden sich für diesen Winkel Werte von 23: 28° bis 23:32°.
Die Deklination lässt sich wie folgt berechnen:
ekliptikale Länge der Sonne: λS
Winkel Ekliptik zu Äquator: ε
Deklination: δ
Rektaszension: RA
|
|
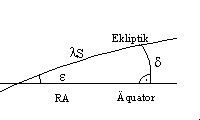 |
sin δ = sin λ * sin ε
tan δ = sin RA * sin ε
|
Sucht man die Deklination für eine Sonnenlänge von z. B. 61° (ca. 22. Mai gregorianisch), so berechnet sich dies wie folgt:
sin δ = sin (sin 61° * sin 23.45°) = 20.3683° oder 20° 22' 6''
Sonnenhöchststand / Sonnentiefststand
Die Sonne kreuzt auf ihrer täglichen Bahn zweimal den Zentralmeridien, das ist jener Grosskreis, der vom Nordpunkt des Aquators über Pol, Zenit und über den Südpunkt zurück zum Nordpunkt geht.
Sonnenhöchststand: 90° - φ + δ (Mittags)
Sonnentiefststand: 90° - φ - δ (Mitternacht)
Der Stundenwinkel beträgt dann 0 bzw. 180 Grad
Bestimmung des Zeitpunkts einer vorgegebenen Sonnenhöhe
Um den Zeitpunkt zu ermitteln, an dem die Sonne einen bestimmten Abstand über oder unter dem Horizont erreicht hat, muss man den Winkel zwischen Zentralmeridian und Sonne, den sogenannten Stundenwinkel τ berechnen. Anzugeben ist die gewünschte Sonnenhöhe h.
In diesem oben abgebildeten nautischen Dreieck sind nun gegeben:
Der Abstand Pol zu Zenit (PZ): 90- φ
Der Abstand Pol zu Sonne (PS): 90- δ
Der Abstand Zenit zu Sonne (ZS): 90- h;
Gesucht ist der Stundenwinkel τ
Nach dem Seitencosinussatz gilt:
| cos τ |
= |
sin h - sin δ sin φ |
| cos δ cos φ |
|
Tag- und Nachtstunden: Um die Tagstunden oder die Nachtstunden zu ermitteln, muss man den Stundenwinkel für die Sonnenhöhe 0 ermitteln.
Beispiel:
φ = 41
δ = 20.368 (Länge der Sonne: 61° in der Ekliptik)
h = 0
cos τ = (sin 0 - sin δ sin φ) / (cos δ cos φ)
τ = 108.828° = 7:15 Stunden
Dieser Wert zeigt die Zeit zwischen Sonnenaufgang und Mittag an.
Auf die gleiche Weise kann man auch die Zeit von Sonnenuntergang bis Mitternacht berechnen. Man muss nur das Vorzeichen von δ vertauschen:
τ = 71.173° = 4:45 Stunden
Gebetszeiten in der Nacht: Das Nachtgebet beginnt, wenn die Sonne nach Sonnenuntergang 17 - 19 Grad unter dem Horizont steht und endet, wenn sie nach ihrem Tiefststand zu Mitternacht wieder 17 - 19 Grad erreicht hat. Man muss den Stundenwinkel für die entsprechende Sonnenhöhe ermitteln.
Beispiel:
φ = 41
δ = 20.368 (Länge der Sonne: 61° in der Ekliptik)
h = -17
cos τ = (sin 0 - sin δ sin φ) / (cos δ cos φ)
τ = 108.826° = 7:15 Stunden
Dieser Wert zeigt die Zeit zwischen Sonnenaufgang und Mittag an.
Auf die gleiche Weise kann man auch die Zeit von Sonnenuntergang bis Mitternacht berechnen. Man muss nur das Vorzeichen von δ vertauschen:
τ = 71.173° = 4:45 Stunden
Bestimmung der Sonnnenhöhe für bestimmte Schattenlängen
Der Beginn des Zeitrahmens des Nachmittagsgebets (asr) wird durch die Länge des Schattens eines Gegenstandes bestimmt.
Die Zeit für das Nachmittagsgebet ist gekommen, wenn der Schatten eines Gegenstandes gleich ist dem Schatten zu Mittag zuzüglich der Länge des schattenwerfenden Gegenstandes. (asr I)
oder
Die Zeit für das Nachmittagsgebet ist gekommen, wenn der Schatten eines Gegenstandes gleich ist dem Schatten zu Mittag zuzüglich der doppelten Länge des schattenwerfenden Gegenstandes. (asr II)
Als erstes ist herauszufinden, wie hoch die Sonne über dem Horizont stehen muss, um damit die genannten Bedingungen erfüllt werden.
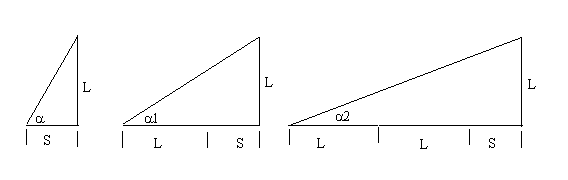
L: Länge des schattenwerfenden Gegenstandes
S: Schattenlänge zu Mittag
Die folgenden Berechnungen sind nach den Regeln der ebenen Trigonometrie durchzuführen:
| |
= |
1 |
= |
1 |
| cot α + 1 |
cot (90° + δ - φ) + 1 |
| |
= |
1 |
= |
1 |
| - tan (δ - φ) + 1 |
tan (φ - δ) + 1 |
| |
| tan h |
= |
1 / (tan (φ - δ) + 1) |
|
|
|
|
| |
= |
1 |
= |
1 |
| cot α + 2 |
cot (90° + δ - φ) + 2 |
| |
= |
1 |
= |
1 |
| - tan (δ - φ) + 2 |
tan (φ - δ) + 2 |
| |
| tan h |
= |
1 / (tan (φ - δ) + 2) |
|
|
|
Mit der so ermittelten Sonnenhöhe kann nun der Stundenwinkel und somit der Zeitpunkt des Nachmittagsgebetes errechnet werden.
Beispiel:
φ = 41
δ = 20.366 (Länge der Sonne: 61° in der Ekliptik)
[Sonnenhöhe zu Mittag = 90 - φ + δ = 69,366]
Sonnenhöhe für Asr I
tan h = 1 / (tan (41 - 20.366) + 1)
h = 36 Grad
Sonnenhöhe für Asr II
tan h = 1 / (tan (41 - 20.366) + 2)
h = 22.82 Grad
Qibla und Sonnenrichtung
In vielen Kalendern findet sich auch eine Spalte, die anzeigt, zu welcher Tageszeit die Sonne in Richtung der Qibla steht.
Die Berechnung der Qibla
Die Berechnung der Qibla ist ein eigenes Problem. Die theoretisch Lösung lautet wie folgt:
gegeben ist:
| |
B-Mekka |
Der Breitengrad von Mekka: |
| B-Ort |
Der Breitengrad des Ortes: |
| ΔL |
Die Differenz im Längengrad
zwischen Mekka und Ort: |
ΔL |
gesucht ist:
| q |
= |
sin ΔL
|
|
tan B-Mekka
cos B-Ort
-
sin B-Ort
cos ΔL
|
In islamischen Quellen wird in der Regel der Winkel angegeben, den die Gebetsrichtung mit der Südrichtung bildet, also der Komplementärwinkel von q zu 180°.
Schon bei Battani (ca. 860 - 929 n. Chr.) findet sich Näherungsformeln für dieses Problem. Dies sagt aber nicht viel darüber aus, wie genau die Gebetsrichtung für konkrete Örtlichkeiten bekannt war. Die Bestimmung des Längengrades war kein leicht zu lösendes Problem. Genauere Untersuchungen zum Beispiel über die Ausrichtung der Moscheen zu verschiedenen Jahrhunderten in den einzelnen islamischen Ländern konnten nicht gefunden werden.
Nun zurück zur Bestimmung des Zeitpunktes, da die Sonne in Gebetsrichtung steht.
In dem nautischen Dreick sind gegeben:
Der Azimuthwinkel S Z P gleich der Qiblarichtung q
Der Abstand Pol zu Zenit (PZ): 90- φ
Der Abstand Pol zu Sonne (PS): 90- δ
Gesucht ist der Stundenwinkel Z P S
Als Zwischenwert ist zuerst der Winkel bei S zu berechnen
| sin S |
= |
sin q cos φ |
| cos δ |
Es gilt dann:
| sin τ |
= |
sin q sin S sin δ sin φ - cos q cos S
|
| 1 - sin q sin S cos δ cos φ
|
Ein anderer Weg, dem bei programmierten Berechnungen zuweilen der Vorzug zu geben ist, besteht darin, zuerst zuerst die Höhe der Sonne über dem Horizont (h) zu berechnen und dann nach den gezeigten Formeln den Stundenwinkel zu bestimmen:
| sin h |
= |
sin φ sin δ - cos δ cos φ cos q cos S
|
| 1 - sin q sin S cos δ cos φ
|