| Startseite | Glossar | Gästebuch | Forum | Impressum | FAQ | Inhalt |
| N A. B | Die Zeit |
| Gliederung |
| |
|
Seitenanfang | Seitenende |
Als natürliches Maß für die Zeit bietet sich der Tag an, die scheinbar gleichmäßige Drehung der Erde um ihre Achse. Die Tageslänge wird definiert als die Dauer von einem Durchgang der Sonne durch den Zentralmeridian bis zum folgenden Durchgang, ein Zeitraum, der schon mit den einfachsten Mitteln recht genau zu bestimmen ist. Der Tag wiederum wird unterteilt in 2 mal 12 Stunden, wobei in alten Zeiten die Zeit von Sonnenuntergang bis Sonnenaufgang in 12 Stunden unterteilt wurde, und dann wieder die Zeit von Sonnenaufgang bis Sonnenuntergang. In Abhängigkeit von den Jahreszeiten entstanden dadurch unterschiedlich lange Tag- und Nachtstunden. Solange zu Terminvereinbarungen Schattenlängen benutzt wurden, mochte dies gerechtfertigt gewesen sein. Allmählich setzten sich dann allerdings gleichmäßig lange Stunden durch.
Der Anfang des bürgerlichen Tages wurde unterschiedlich geregelt. Weitgehend durchgesetzt hat sich inzwischen der Tagesanfang um Mitternacht. Bei Kulturen, die sich am Mondkalender orientieren, beginnt der Tag in der Regel bei Sonnenuntergang oder um 18.00 Uhr.
Diese sogenannte "wahre Sonnenzeit" kann man als die natürlichste Zeit für den Menschen betrachten. Sie wird von genau justierten Sonnenuhren angezeigt.
| |
|
Seitenanfang | Seitenende |
Sehr viel gleichmässiger als die Sonnenzeit ist die Sternzeit. Sie wird abgeleitet aus der Umdrehung der Erde gegenüber dem Sternenhimmel. Ein Sterntag entspricht dem Zeitraum von einem Durchgang des Frühlingspunktes oder eines Fixsternes durch den Meridian bis zum nächstfolgenden Durchgang. Er ist knapp 4 Minuten kürzer als der Sonnentag, im Laufe eines Jahres ergibt dies genau einen Tag, also jene zusätzliche Umdrehung der Erde auf ihrer jährlichen Bahn um die Sonne.
Ausgangspunkt der Sternzeit ist der Schnittpunkt von Himmelsäquator und Ekliptik. Sie ist somit die auf diesen Punkt bezogene Rektaszension des Zenitpunktes. Die Sternzeit wird daher auch als der Stundenwinkel des Frühlingspunktes bezeichnet. Zu einem bestimmten Zeitpunkt hat sie für alle Beobachter auf gleicher geographischer Länge den gleichen Wert.
Die wechselnden Stellungen von Sonne und Mond bewirken Schwankungen des wahren Frühlingspunkt um den mittleren Schnittpunkt von Äquator und Ekliptik. In Strenge muss daher unterschieden werden zwischen der mittleren und der wahren Sternzeit. Von besonderer Bedeutung wurde die auf den Nullmeridian bezogene Sternzeit, die Greenwich Mean Sideral Time (GMST).
| |
|
Seitenanfang | Seitenende |
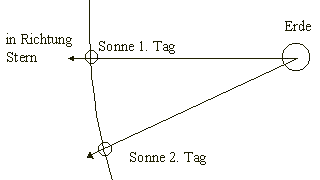 So einfach die wahre Sonnenzeit auch sein mag, einen großen Nachteil hat sie doch: sie ist nicht sehr gleichmäßig. Während sich die Erde einmal um ihre Achse dreht, bewegt sich auch die Sonne auf ihrer Bahn um die Erde ein Stück weiter. Steht nun die Sonne in Erdnähe, so ist ihre Bahngeschwindigkeit größer, sie wird sich in dieser Zeit weiter fortbewegen und der Tag wird dementsprechend länger sein als wenn sie in Erdferne steht und sich demzufolge langsamer bewegt. Auch die Tatsache, daß die Sonne sich bei ihrer scheinbaren Bahn am Himmel je nach Jahreszeit mal über und mal unter dem Himmelsäquator befindet, hat Einfluß auf die Tageslänge.
So einfach die wahre Sonnenzeit auch sein mag, einen großen Nachteil hat sie doch: sie ist nicht sehr gleichmäßig. Während sich die Erde einmal um ihre Achse dreht, bewegt sich auch die Sonne auf ihrer Bahn um die Erde ein Stück weiter. Steht nun die Sonne in Erdnähe, so ist ihre Bahngeschwindigkeit größer, sie wird sich in dieser Zeit weiter fortbewegen und der Tag wird dementsprechend länger sein als wenn sie in Erdferne steht und sich demzufolge langsamer bewegt. Auch die Tatsache, daß die Sonne sich bei ihrer scheinbaren Bahn am Himmel je nach Jahreszeit mal über und mal unter dem Himmelsäquator befindet, hat Einfluß auf die Tageslänge.
Um diese Schwankungen auszugleichen wurde die mittlere Sonnenzeit eingeführt. Es ist eine Zeit, die ausgeht von einer sich mit gleichmäßiger Geschwindigkeit auf einer Kreisbahn am Himmelsäquator bewegenden fiktiven Sonne.
Die mittlere Sonnenzeit kann naturgemäß nicht mehr direkt am Himmel abgelesen werden. Sie wird vielmehr berechnet aus der mittleren Greenwich-Sternzeit, die wiederum, wie oben ausgeführt, aus Beobachtungen von Meridiandurchgängen bestimmt werden kann.
UT: Weltzeit
T: Zeit in julianischen Jahrhunderten bezogen auf den 1. 1. 2000, 12.00 Uhr UT
GMST: Greenwich Mean Sideral Time
T = (JD - 24515454) / 36525
GMST (UT = 0h) = 24110.54841 sec
+ 8640184.812866 * T
+ 0.093104 * T * T
- 0.0000062 * T * T * T
Aus dieser Beziehung läßt sich die Mittlere Zeit für jeden Zeitpunkt berechnen. Die Mittlere Zeit ist also eine Umformung der Sternzeit.
Die Differenz zwischen der wahren Sonnenzeit und der mittleren Sonnenzeit wird als Zeitgleichung (ZGL) bezeichnet. Wie bereits erwähnt hat sie zwei Ursachen:
Anteil der Ekliptikschiefe
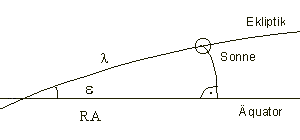
Der Anteil der Ekliptikschiefe an der Zeitgleichung läßt sich einfach erläutern. Wie aus der folgenden Skizze erkenntlich ist, spielt hierbei der Winkel (e), den Ekliptik und Äquator bilden, eine Rolle. Sein Wert ist Schwankungen unterworfen. Für einen bestimmten Zeitpunkt (T) läßt er sich berechnen:
 T: Julianische Jahrhunderte, bezogen auf den 0. 1. 1900, 12.00 UT
T: Julianische Jahrhunderte, bezogen auf den 0. 1. 1900, 12.00 UT
T = (JD - 2415020.0) / 36525
ε = 23°27'08" - 46".81 * T
λ: Länge in Ekliptik
RA: Rektaszension
tan (RA) = tan (λ) * cos (ε)
tan (λ) = tan (RA) / sin (ε)
Wie leicht ersichtlich, ist die Differenz bei einem Winkel von 0°, 90°, 180° und 270° gleich 0 und wird am größten sein bei einem Winkel von 45°, 135°, 225°, und 315°. Sie beträgt dann ca. 2°28', was einem Zeitunterschied von rund 9.87 Minuten entspricht.
Anteil der Anomalie
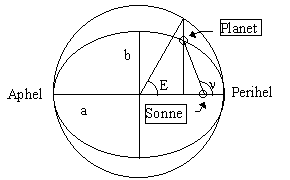
Nach den Keplerschen Gesetzen bewegt sich ein Planet, also auch die Erde auf ihrer Bahn um die Sonne, auf einer elliptischen Bahn, wobei die Verbindungslinie Sonne - Planet in gleichen Zeiträumen gleiche Flächen überstreicht.
Die Form der Ellipse, also ihre Abweichung von der Kreisbahn, wird bestimmt durch die Exzentrizität (e), die das Verhältnis der großen Halbachse (a) zur kleinen Halbachse (b) wiedergibt.
| Es gilt: |
Je kleiner die Exzentrizität, desto mehr gleicht die Ellipse einer Kreisbahn. Beim Kreis selbst ist e = 0, da a = b. Eine Parabel hat die Exzentrizität 1.
Die Erdbahn hat eine Exzentrizität von ca. 0.01675, weicht also nur gering von einer Kreisbahn ab. Dieser Wert ist langperiodischen Schwankungen unterworfen und kann für einen bestimmten Zeitpunkt (T) nach folgender Formel bestimmt werden.:
T: julianische Jahrhunderte, bezogen auf den 0.1.1900, 12.00 Uhr UT
e = 0.016751 - 0.000042 * T
Für die Zeitgleichung ist nun von Bedeutung die Differenz zwischen der mittleren Anomalie und der wahren Anomalie. Unter mittlerer Anomalie versteht man den Winkelabstand vom Perihel, den die Sonne (geozentrisch gesehen) hätte, würde sie sich auf einer Kreisbahn mit konstanter Geschwindigkeit um die Erde bewegen. Die wahre Anomalie beschreibt den wahren Winkelabstand auf der elliptischen Bahn. Die wahre Anomalie kann aus der mittleren Anomalie (M) nur über eine Hilfsgröße, der exzentrischen Anomalie (E) berechnet werden. Man erhält sie nach der folgenden Keplerschen Gleichung:
E = M + sin (E)
Diese Gleichung läßt sich nur iterativ auflösen.
Aus der exzentrischen Anomalie (E) läßt sich nun die wahre Anomalie (ν) ermitteln:
 |
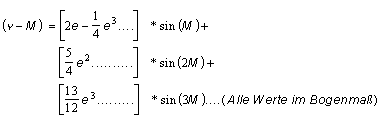
Die größte auftretende Differenz (bei einer wahren Anomalie von ca. 89°) beträgt rund 1°55', was einem Zeitunterschied von ca. 7.67 Minuten entspricht.
Die folgende Skizze soll den Einfluß der beiden Faktoren auf die Zeitgleichung noch einmal verdeutlichen:
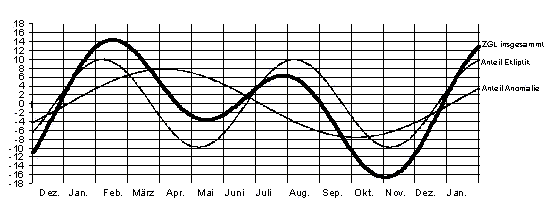
Wahre Zeit + ZGL = Mittlere Zeit
Die grössten Abweichungen der Mittleren Zeit von der Wahren Zeit sind:
ca. 11. Februar + 14 min 14 sec
ca. 14. Mai - 3 min 45 sec
ca. 26. Juli + 6 min 21 sec
ca. 3. Novemb. - 16 min 19 sec
In einigen Quellen wird die Zeitgleichung auch definiert als: ZGL = Wahre Zeit - Mittlere Zeit.
Die obige Skizze müßte also um die x-Achse gespiegelt werden.
Die Zeitgleichung läßt sich auch über die mittlere Sonne (L) direkt für einen bestimmten Zeitpunkt (T) berechnen:
T: julianische Jahrhunderte, bezogen auf den 0. 1. 1900, 12.00 Uhr
T = (JD - 2415020.0) / 36525
L = 279.966778° + 36000° * T + 2768.3" * T + 1.089" * T2
ZGL = 105.1 * sin (L) - 596.2 * sin (2L) - 4.3* sin (3L) + 12.7 * sin (4L)
+ 429.2 * cos (L) + 2.1 * cos (2L) - 19.3 * cos (3L) (Ergebnis in Sekunden)
Mittlere Zeit = Wahre Zeit + ZGL
| |
|
Seitenanfang | Seitenende |
Von besonderer Bedeutung war die auf den Null-Meridian bezogene mittlere Zeit, die Greenwich Mean Time (GMT). Immer dann, wenn Angaben allgemein gültig sein sollten, z.B. in astronomischen Jahrbüchern, fand sie Verwendung. Eine allfällige Umrechnung auf Zonenzeiten war ja kein Problem. Sie wurde so zu einer universellen Zeit. Allerdings waren verschiedene Definitionen von GMT in Umlauf. In der Astronomie wurde GMT sogar von Mittag bis Mittag gerechnet.
| |
|
Seitenanfang | Seitenende |
Wegen all dieser Verwirrungen im Zusammenhang mit GMT wurde daher 1926 wurde daher die Weltzeit (Universal Time, UT) als Ersatz für die GMT eingeführt. Auch von ihr gibt es verschiedene Varianten:
Der Unterschied zwischen den verschiedenen Weltzeiten liegt im Bereich von Millisekunden.
| |
|
Seitenanfang | Seitenende |
Alle bisher genannten Zeiten sind definiert in Abhängigkeit zur Dauer der Erdrotation. Diese ist allerdings nicht konstant. Zum einen ist sie kurzfristigen Schwankungen unterworfen, zum anderen verlangsamt sie sich stetig. Jede Zeitskala, die auf der Erdrotation basiert, muss daher unregelmässig sein. Physiker und Astronomen standen somit vor der Notwendigkeit, ein absolut gleichförmiges Zeitmaß zu finden. Dies führte zur Einführung der Ephemeridenzeit. Nach der in anderem Zusammenhang bereits genannten Formel von Newcomb [siehe: Die Akzeleration] läßt sich die mittlere Länge der Sonne L wie folgt bestimmen:
L = 279.6966778° + 36000° * T + 2768.13" * T + ......
T ist hier die Zeit in julianischen Jahrhunderten seit dem 0. 1. 1900, 12.00 Uhr.
Hieraus ist zum einen zu sehen, daß die Sonne am 31. Dezember 1900 um 12.00 Uhr eine mittlere Länge von 279.6966778° hatte. Wichtiger in diesem Zusammenhang ist allerdings, daß diese Formel zeigt, daß die Sonne in 100 julianischen Jahren, d.h. in 36525 Tagen, 100 mal einen Kreis von 360° zurücklegt und zusätzlich noch 0.768925°. Mit einer einfachen Dreisatzrechnung läßt sich nun die genaue Dauer einen Sonnenumlaufs von 360°, d.h. eines tropischen Jahres, bezogen auf die Verhältnisse des 0. Januars 1900 feststellen:
36525 Tage gleich 3 155 760 000 Sekunden entsprechen 36 000.768925 Grad
x Sekunden entsprechen 360 Grad
x = 31 556 925. 9747 Sekunden
Diese Relation bildet nun die Definition der Ephemeridensekunde. Sie ist der 31 556 925.9747ste Teil des Tropischen Jahres, bezogen auf die Verhältnisse des genannten Datums. Diese Sekunde wurde sozusagen für alle Zeiten fest eingefroren und bildet nun die Einheit der Ephemeridenzeit, die den meisten astronomischen Formeln zugrunde liegt. Sie wurde so gelegt, daß 1900 Ephemeridenzeit und Weltzeit nahezu übereinstimmen.
Aus dieser Beziehung läßt sich auch die Dauer des tropischen Jahres zu diesem Zeitpunkt feststellen: 365d 5h 48m 45.97s.
| |
|
Seitenanfang | Seitenende |
Für die immer exakter werdenden Forschungen der Physiker erwies sich die aufgezeigte Definition einer gleichmäßigen Zeit im Laufe der Jahrzehnte als nicht sehr genau und praktikabel. Im Jahre 1967 beschloss die 13. Internationale Generalkonferenz für Masse und Gewichte die Einführung einer Atomsekunde, die folgendermaßen definiert ist:
Eine Sekunde ist das 9 192 631 770-fache der Periodendauer der dem Übergang zwischen den beiden Hyperfeinstrukturniveaus des Grundzustandes von Atomen des Nuklids Caesium 133 entsprechenden Strahlung.
Damit wurde die Zeit erstmals in das Internationale System der Masse und Gewichte (SI) aufgenommen.
Diese so definierte SI-Sekunde bildet die Einheit der 1972 eingeführten Atomzeit (TAI). Die Atomsekunde war so festgelegt worden, dass sie praktisch die gleiche Dauer wie die Ephemeridensekunde hat. Andererseits wurde die Atomzeit so eingerichtet, dass sie am 1. Januar 1958 mit der Weltzeit (UT) übereinstimmte. Ephemeridenzeit und Atomzeit unterscheiden sich daher um einen konstanten Faktor.
ET = TAI + 32.184 sec.
Rund 200 Atomuhren, verstreut über die gesamte Erdoberfläche, melden derzeit ihre Messergebnisse dem Bureau International des Poid et Mesures (BIPM) in Sevres, Frankreich. Dort wird dann die genaue Atomzeit berechnet.
| |
|
Seitenanfang | Seitenende |
TDT, TDB
Nach den Erkenntnissen der Relativitätstheorien ist die Zeit keine unabhängige Grösse sondern steht immer in Relation zu einem Bezugssystem. Diese relativistischen Effekte berücksichtigen die 1984 eingeführten Dynamischen Zeiten, die sich auf die dynamischen Gesetze der Planetenbewegungen im Sonnensystem beziehen, die wiederum auf der Definition eines Koordinaten- bzw. Bezugssystems beruhen. Bei der Terrestrial Dynamical Time (TDT) dient die Erde als Bezugskörper, der Bezugspunkt der Baryzentric Dynamical Time (TDB) ist der Schwerpunkt des Sonnensystems. Sie weicht von der TDT um nicht mehr als 0.002 sec ab.
Diesen dynamischen Zeiten liegt als Einheit die SI-Sekunde zugrunde. Sie lösten die Ephemeridenzeit als Grundlage der Zeitrechnung ab. Im Interesse einer Kontinuität zwischen Ephemeridenzeit und Dynamischer Zeit wurde die Differenz zur Atomzeit ebenfalls auf 32.184 Sekunden festgelegt:
TDT = ET = TAI + 32.184 sec
Weitere Dynamische Zeitskalen
Im Jahre 1991 wurden von der Internationalen Astronomischen Vereinigung (IAU) die dynamischen Zeitskalen weiter präzisiert:
| |
|
Seitenanfang | Seitenende |
Zum Abschluss nun endlich die Zeit, die heute eine genau gehende Uhr (z.B. eine Funkuhr) anzeigt, die koordinierte Weltzeit (UTC). Die Dauer der Sekunde ist gleich der Atomsekunde, mit der Atomzeit läuft sie also im gleichen Takt. Andererseits weicht sie von der Weltzeit (UT) um nicht mehr als 0.9 Sekunden ab. Dies wird erreicht durch Schaltsekunden, die bei Bedarf Ende Juni oder Ende Dezember eingefügt werden. Atomzeit und koordinierte Weltzeit unterscheiden sich also immer um eine volle Anzahl von Sekunden.
Ist die Uhrzeit definiert in Abhängigkeit vom Sonnenstand, so kann sie nur für eine bestimmten Ort beziehungsweise für alle Orte, die mit diesem auf dem gleichen Längengrad liegen, gelten, ist also immer eine lokale Zeit. Bis ins 19. Jahrhundert wurde dies auch als natürlich und selbstverständlich betrachtet. Bei immer besser werdenden Kommunikationsmöglichkeiten und immer schneller werdenden Verkehrsverbindungen brachte die Vielzahl lokaler Zeiten jedoch Probleme. Man stelle sich nur vor, wie verwirrend es gewesen sein musste, wenn z.B. auf dem Wiener Bahnhof ein Zug aus St. Peterburg mit dortiger Ortszeit, ein Zug aus Berlin mit Berliner Ortszeit und noch weitere Züge aus anderen Regionen mit ihren jeweiligen Ortszeiten einliefen.
Im 19. Jahrhundert wurden zuerst in einer Reihe von Ländern einheitliche Landeszeiten eingeführt, die sich nach der Ortszeit der jeweiligen Hauptstadt richteten. Gegen Ende dieses Jahrhunderts führten dann die meisten Länder eine Zonenzeit ein. Die einzelnen Zonen differieren um je eine volle Stunde, in Ausnahmefällen auch einmal um eine halbe Stunde, ihre Grenzen gehen in der Regel mit den Staatsgrenzen konform. Lediglich in Staaten, die über eine grosse Ost-Westausdehnung verfügen, finden sich mehrere Zonen. So gilt in dem Vereinigten Königreich von Grossbritannien und Nordirland die westeuropäische Zeit, die sich nach dem Null-Meridian richtet. Gemeinhin wurde sie als Greenwich Mean Time (GMT) bezeichnet, nach dem Londoner Stadtteil, in dem die Sternwarte liegt, durch die der Null-Meridian geht. Die in Deutschland gültige Normalzeit, die Mitteleuropäische Zeit (MEZ, CET, Central European Time), entspricht der Zeit des 15. östlichen Längengrades, der Deutschland allerdings nur am Rande (bei Görlitz) berührt. MEZ = GMT + 1 Stunde. Die in der Türkei geltende Normalzeit, die Osteuropäische Zeit, differiert um zwei Stunden von der GMT, in Persien unterscheidet sich die Normalzeit um dreieinhalb Stunden von GMT. Im Deutschen Reich ist die Mitteleuropäische Zeit seit dem 1. April 1893 die verbindliche Normalzeit.
Zur Einsparung von Energie oder mit anderen Begründungen wurden in einigen Staaten immer wieder, besonders häufig in Kriegszeiten, eine Sommerzeit eingeführt, in der dann die Uhren gegenüber der Normalzeit um eine Stunde vorgestellt wurden.
Die lange Zeit in der Sovietunion geltende "Dekretzeit" (nach einem Dekret Stalins) verschob die Zeit sogar um zwei Stunden bezogen auf die jeweilige Zonenzeit in diesem grossen Reich, entsprach also einer doppelten Sommerzeit.
Sommerzeiten in Österreich
| 1916 | 30. April | 23.00 Uhr | bis | 30. September | 01.00 Uhr | Quelle |
| 1917 | 16. April | 02.00 Uhr | bis | 17. September | 03.00 Uhr | Quelle |
| 1918 | 15. April | 03.00 Uhr | bis | 16. September | 03.00 Uhr | Quelle siehe auch:Quelle |
| 1919 | In diesem Jahr wurde durch Vollzugsanweisung vom 20. April eine Sommerzeit eingeführt (Quelle), durch Vollzugsanweisung vom 26. Apriil wieder abgeschafft (Quelle). |
|||||
| 1920 | 5. April | 02.00 Uhr | bis | 13. September | 03.00 Uhr | Quelle |
| von 1921 bis 1939 gab es keine Sommerzeit | ||||||
| 1940 | 01.April | 02.00 Uhr | Nach dem Anschluss Österreichs an das Deutsche Reich bis zum Kriegsende 1945 galten die deutschen Zeitverordnungen auch in Österreich | |||
| 1941 | durchgehend bis | |||||
| 1942 | 02.November | 03.00 Uhr | ||||
| 1943 | 29. März | 02.00 Uhr | bis | 04. Oktober | 03.00 Uhr | |
| 1944 | 03. April | 02.00 Uhr | bis | 04. Oktober | 03.00 Uhr | |
| 1945 | 02. April | 02.00 Uhr | bis | 23. April, regionale Abweichungen | ||
| 1946 | 14. April | 02.00 Uhr | bis | 07. Oktober | 03.00 Uhr | Quelle Quelle |
| 1947 | 06. April | 02.00 Uhr | bis | 05. Oktober | 03.00 Uhr | Quelle Quelle |
| 1948 | 18. April | 02.00 Uhr | bis | 03. Oktober | 03.00 Uhr | Quelle Quelle |
| von 1949 bis 1979 gab es keine Sommerzeit | ||||||
| 1980 | 6. April | 00.00 Uhr | bis | 27. September | 24.00 Uhr | Quelle |
| 1981 | 29. März | 02.00 Uhr | bis | 27. September | 03.00 Uhr | Quelle |
| 1982 | 28. März | 02.00 Uhr | bis | 26. September | 03.00 Uhr | |
| 1983 | 27. März | 02.00 Uhr | bis | 25. September | 03.00 Uhr | Quelle |
| 1984 | 25. März | 02.00 Uhr | bis | 30. September | 03.00 Uhr | |
| 1985 | 31. März | 02.00 Uhr | bis | 29. September | 03.00 Uhr | |
| 1986 | 30. März | 02.00 Uhr | bis | 28. September | 03.00 Uhr | Quelle |
| 1987 | 29. März | 02.00 Uhr | bis | 27. September | 03.00 Uhr | |
| 1988 | 27. März | 02.00 Uhr | bis | 25. September | 03.00 Uhr | |
| 1989 | 26. März | 02.00 Uhr | bis | 24. September | 03.00 Uhr | Quelle |
| 1990 | 25. März | 02.00 Uhr | bis | 30. September | 03.00 Uhr | Quelle |
| 1991 | 31. März | 02.00 Uhr | bis | 29. September | 03.00 Uhr | |
| 1992 | 29. März | 02.00 Uhr | bis | 27. September | 03.00 Uhr | |
| 1993 | 28. März | 02.00 Uhr | bis | 26. September | 03.00 Uhr | Quelle |
| 1994 | 27. März | 02.00 Uhr | bis | 25. September | 03.00 Uhr | |
| 1995 | 26. März | 02.00 Uhr | bis | 24. September | 03.00 Uhr | Quelle |
| 1996 | 31. März | 02.00 Uhr | bis | 31. Oktober | 03.00 Uhr | u. s. w. |
| Seit dem Jahre 1996 beginnt die Sommerzeit jedes Jahr am letzten Sonntag im März um 02.00 Uhr (gleich 01.00 Uhr Weltzeit) und endet am letzten Sonntag im Oktober um 03.00 Uhr (gleich 01.00 Uhr Weltzeit). Dies erfolgte in in Umsetzung der Richtlinie 94/21/EG des Europäischen Parlaments und des Rates vom 30. Mai 1994. Diese Richtlinie entspricht der späteren EU Richtlinie 2000/84/EG Die Grundsätzliche Regelung der Sommerzeit erfolgte durch das Zeitzählungsgestz vom 27. Jänner 1976 [ Quelle], geändert durch Bundesgesetz vom 20. Jänner 1981 [ Quelle] |
||||||
Sommerzeit in Deutschland
| 1916 | 30. April | 23.00 Uhr | bis | 01. Oktober | 01.00 Uhr | Quelle: PTB |
| 1917 | 16. April | 02.00 Uhr | bis | 17. September | 03.00 Uhr | |
| 1918 | 15. April | 02.00 Uhr | bis | 16. September | 03.00 Uhr | |
| von 1919 bis 1939 gab es keine Sommerzeit | ||||||
| 1940 | 01. April | 02.00 Uhr | Quelle | |||
| 1941 | durchgehend bis | Quelle | ||||
| 1942 | 02.November | 03.00 Uhr | Quelle | |||
| 1943 | 29. März | 02.00 Uhr | bis | 04. Oktober | 03.00 Uhr | Quelle |
| 1944 | 03. April | 02.00 Uhr | bis | 02. Oktober | 03.00 Uhr | Quelle |
| 1945 | 02. April | 02.00 Uhr | bis | 16. September | 03.00 Uhr | nur Westzonen |
| 1945 | 02. April | 02.00 Uhr | bis | 01. Mai | Ostzone | |
| 1945 | 01. Mai | 02.00 Uhr | bis | 25. September | 0.3.00 Uhr | doppelte Sommerzeit, nur Ostzone |
| 1945 | 25. Sept. | bis | 18. November | Sommerzeit, nur Ostzone | ||
| 1946 | 14. April | 02.00 Uhr | bis | 07. Oktober | 03.00 Uhr | |
| 1947 | 06. April | 02.00 Uhr | bis | 10. Mai | 03.00 Uhr | einfache Sommerzeit |
| 11. Mai | 03.00 Uhr | bis | 29. Juni | 03.00 Uhr | doppelte Sommerzeit | |
| 29. Juni | 03.00 Uhr | bis | 05. Oktober | 03.00 Uhr | einfache Sommerzeit | |
| 1948 | 18. April | 02.00 Uhr | bis | 03. Oktober | 03.00 Uhr | |
| 1949 | 10. April | 02.00 Uhr | bis | 02. Oktober | 03.00 Uhr | |
| von 1950 bis 1979 gab es keine Sommerzeit | ||||||
| 1980 | 6. April | 02.00 Uhr | bis | 28. September | 03.00 Uhr | BRD und DDR |
| Seit 1981 hat Deutschland die gleiche Regelung wie Österreich und die Schweiz.
Von 1981 bis 1995 begann in Deutschland die Sommerzeit am letzten Sonntag im März um 2.00 Uhr MEZ und endet am letzten Sonntag im September um 3.00 Uhr MESZ. Seit 1996 beginnt in Deutschland die Sommerzeit am letzen Sonntag im März um 2.00 Uhr MEZ und endet am letzten Sonntag im Oktober um 3.00 Uhr MESZ. Quelle: Physikalisch-Technische Bundesanstalt (PTB) http://www.ptb.de .. Fachabteilungen > Abt. 4 Optik > 4.4 Zeit und Frequenz > 4.41 Zeitnormale > Darstellung der gesetzlichen Zeit: Ausführliche Informationen zur gesetzlichen Zeit |
||||||
Sommerzeit in der Schweiz
| 1916 | 14. Juni | bis | 1. Oktober | ?? | ||
| 1941 | 5. Mai | 01.00 Uhr | bis | 6. Oktober | 02.00 Uhr | Quelle |
| 1942 | 4. Mai | 01.00 Uhr | bis | 4. Oktober | 02.00 Uhr | Quelle |
| 1981 | 29. März | 02.00 Uhr | bis | 27. September | 03.00 Uhr | Quelle |
| Seit 1981 hat die Schweiz die gleiche Zeitregelung wie Österreich und Deutschland. Quelle Quelle | ||||||
Durch die Richtlinie 2000/84/EG des Europäischen Parlamentes wurde die Sommerzeit für alle Länder der Europäischen Union eingeführt. Sie beginnt am letzten Sonntag im März um 1.00 Uhr UTC, das entspricht 2.00 Uhr MEZ und endet am letzten Sonntag im Oktober um 1.00 Uhr UTC, das entspricht 3.00 Uhr MESZ. Internetlink
Die Uhrzeiten der Tabellen sind wie folgt zu verstehen:
Am 31. März 1996 ist der Zeitpunkt 2.00 Uhr MEZ ist identisch mit dem Zeitpunkt 3.00 Uhr MESZ oder 1.00 Uhr Weltzeit
Am 31. Oktober 1996 ist der Zeitpunkt 3.00 Uhr MESZ ist identisch mit dem Zeitpunkt 2.00 Uhr MEZ oder 1.00 Uhr Weltzeit
| |
|
Seitenanfang | Seitenende |
Der vorstehende Überblick über Zeitskalen will und kann nicht in Konkurrenz treten mit Veröffentlichungen von Physikern und Astronomen. Er stellt lediglich den Versuch dar, verschiedene Zeitsysteme, auf die auch in chronologischen Abhandlungen immer wieder hingewiesen wird, in einfacher und populärer Form vorzustellen.
Da in Fragen der Chronologie eine übergrosse Genauigkeit meist nicht erforderlich ist, können folgende Zeiten gleichgesetzt werden:
| |
|
Seitenanfang | Seitenende |
Genauere Definitionen der verschiedenen Zeitsysteme finden sich u. a. in :"Explanatory Supplement to the Astronomical Almanac, edited by P. K. Seidelmann.[Seidelmann 1992]
Die mathematischen Gleichungen wurden entnommen dem Werk von Oliver Montenbruck: Grundlagen der Ephemeridenberechnung, eine auch für Laien verständliche Einführung in die Gesetze der Himmelsmechanik. [Montenbruck1987]
Grundsätzlich sei ferner verwiesen auf folgende Internetseiten:
| |
Seitenanfang |
| Startseite | Glossar | Gästebuch | Forum | Impressum | FAQ | Inhalt |