| Startseite | Glossar | Gästebuch | Forum | Impressum | FAQ | Inhalt |
| N A. B | Die Akzeleration |
| Gliederung |
Tag, Monat und Jahr sind die in der Chronologie wichtigen Einteilungen des scheinbar stetig dahinfliessenden Zeitablaufes. Lange Zeit ging man davon aus, dass diese Grössen bei allen kurzfristigen Schwankungen auf Dauer gesehen konstant seien. Der englische Astronom Halley, einer breiteren Öffentlichkeit vor allem bekannt durch die Wiederentdeckung des nach ihm benannten Kometen, stellte bei Bahnberechnungen fest, dass der Mond am Himmel stets ein wenig gegenüber der errechneten Position voraus war, also scheinbar schneller lief als er es nach den Gravitationsgesetzen sollte. Dieses Phänomen nannte man "Akzeleration (Beschleunigung) des Mondes". Genaue Messungen zeigten auch bei den Planeten einen ähnlichen Beschleunigungseffekt. Der Grund hierfür konnte also nicht in der Mondbahn liegen, er musste universeller Natur sein. Erst geraume Zeit später stellte man fest, dass die Ursache darin lag, dass die Zeit selbst, so man sie in Abhängigkeit von der Erdumdrehung sieht, unregelmässig ist. Da sich die Erde im Laufe der Zeit immer langsamer dreht, scheinen sich die Gestirne am Himmel immer schneller zu bewegen.
| |
|
Seitenanfang | Seitenende |
Bei den folgenden Überlegungen wird immer wieder zurückgegriffen werden auf Bahnberechnungen von Sonne und Mond. Daher seien die grundlegenden Formeln von Newcomb, die ja auch die Ephemeriden-Zeit definieren, hier noch einmal wiedergegeben[ 1 ]. Ihnen gegenübergestellt werden jene Formeln, die Ahnert seinen Tabellen zugrunde legt, da bei ihnen die Akzeleration direkt berücksichtigt wird [ 2 ]
Mittlere Länge der Sonne:| nach Newcomb: | ||
| L = 279.6966778 + 36000.768925 * T + 0.0003025 * T2 | ||
| (T bezogen auf 1900, Januar 0, 12.00 Uhr) | ||
| nach Ahnert: | ||
| L = 279.204 + 36000.769 * T + 0.00065 * T2 | ||
| (T bezogen auf 1900, Januar 0, 00.00 Uhr) | ||
| nach Newcomb: | ||
| l = 270.434164 + 481267.883142 * T - 0.001133 * T2 | ||
| (T bezogen auf 1900, Januar 0, 12.00 Uhr) | ||
| nach Ahnert: | ||
| l = 329.135 + 481267.887 * T + 0.00343 * T2 | ||
| (T bezogen auf 1800, Januar 0, 00.00 Uhr) | ||
| z = 5038.3" * T - 1.1" * T2 z = 1.399528° * T - 0.00031° * T2 |
| z = 5026.87" * T + 1.11" * T2 z = 1.39635 * T + 0.0003083° * T2 |
Aus diesen Formeln können nun die Monats- und Jahreslängen abgeleitet werden, wobei die Formeln von Newcomb benutzt werden, nach dessen Berechnungen ja die Zeit definiert ist.:
| Das tropische Jahr: | 36525 * 360 / 36000.768925 = 365.24219878173 (Tage) |
| das sind 365d 5h 48m 45.9747s | |
| Der tropische Monat: | 36525 * 360 / 481267.883142 = 27.32158214 (Tage) |
| das sind 27d 7h 43m 4.7s | |
| Der synodische Monat: | 360 / (360 / 27.32158214 - 360 /365.242198781) = 29.53058868 (Tage) |
| das sind 29d 12h 44m 2.86s |
Ein Julianisches Jahrhundert (36525 Tage) enthält 1236.853095 synodische Monate.
Aus diesen Daten können auch die mittleren Bahngeschwindigkeiten von Sonne und Mond berechnet werden:
| Sonne: | 1 Grad gleich | 1.014561663 Tage | 1 Tag gleich | 0.985647335 Grad | ||
| Mond: | 1 Grad gleich | 0.075893283 Tage | 1 Tag gleich | 13.17639653 Grad |
| |
|
Seitenanfang | Seitenende |
Wie bereits erwähnt ist die Zeit, so man als Massstab die Erdrotation nimmt, keineswegs gleichmässig. Die von Sonne und Mond ausgehenden Anziehungskräfte sind es, die in erster Linie zu Unregelmässigkeiten der Erdrotation führen
Fluktuationen: Vermutlich infolge von Massenverlagerungen im Erdinneren rotiert die Erde über Jahrzehnte hinweg einmal etwas schneller, dann wieder etwas langsamer. Die grössten bisher festgestellten Abweichungen der Tageslänge vom Mittelwert betrugen -0.005 sec (1871) bzw. +0.002 sec (1907). Die Fluktuationen können sich zwar im Laufe mehrerer Jahrzehnte zu beachtlichen Abweichungen aufsummieren, gleichen sich jedoch über grössere Zeiträume hinweg immer wieder aus.
Jahreszeitliche Schwankungen: Sie werden wahrscheinlich durch jahreszeitliche Luftmassenverlagerungen, Abschmelzvorgängen an den Polen usw. verursacht. Die Abweichungen erreichen im März mit +0.0010 sec und im August mit -0.0011 sec ihr Maximum bzw. Minimum.
Säkulare Schwankungen: Für die Chronologie von Bedeutung sind jedoch ausschliesslich die säkularen Änderungen der Erdrotation. Bewirkt insbesondere durch die Gezeitenreibung an den flachen Randmeeren verlangsamt sich die Rotationsgeschwindigkeit der Erde stetig mit einer Zunahme der Tageslänge von ca. 0.0016 sec pro Jahrhundert.
Die dem Schreiber bekannte Literatur bezüglich der Auswirkung der Akzeleration auf Jahreslänge, Monatslänge, Differenz zwischen UT und ET ist widersprüchlich. Die entsprechenden Stellen seien hier zitiert:
dtv-Atlas zur Astronomie, S. 49: Säkulare Schwankungen: Durch Gezeitenreibung an den flachen Randmeeren verlangsamt sich die Erdrotation. Die Tageslänge nimmt pro Jahrhundert um 0.0016 sec zu. [ 3 ]
Ahnert, Tafeln, S. 7: Bei der Berechnung chronologischer Tafeln, die einige Jahrtausende zurückreichen sollen, ist die Berücksichtigung der säkularen Akzeleration (Beschleunigung) in den Bewegungen von Sonne, Merkur, Venus und Mars erforderlich, die von der allmählichen Abnahme der Rotationsgeschwindigkeit der Erde herrühren. Diese Verlangsamung der Erdrotation, die mit einer Zunahme der Tageslänge um 0.0016 Sekunden im Jahrhundert gleichbedeutend ist, wird durch die Gezeitenreibung verursacht, d.h. durch den Widerstand, den die Flutwelle an den Küsten und in den flachen Randmeeren erfährt. Die Vernachlässigung dieser Akzeleration würde um das Jahr 2000 v. u. Z. in den Längen der Sonne einen Fehler von -1° hervorrufen. Bei den heliozentrischen Längen von Merkur, Venus und Mars wären die Fehler schon im Jahre 1000 v. u. Z. -1.5°, -0.8° bzw. -0.4°. Der Mond erleidet ausserdem eine reelle säkulare Verlangsamung seiner Umlaufgeschwindigkeit, die sich dem aus der Abnahme der Rotationsgeschwindigkeit der Erde herrührenden Akzelerationseffekt überlagert. Die Nichtberücksichtigung der aus diesen beiden Ursachen resultierenden säkularen Änderung der Mondbewegung würde die Mondlängen um das Jahr 2000 v. u. Z. bereits um -5° verfälschen. Die säkulare Akzeleration des Mondes hat als erster Halley 1693 bei der Bearbeitung antiker und neuerer Finsternisse gefunden.[ 4 ]
Zwei unterschiedliche Formeln benutzt Frank P Thielen in seinem astronomischen Computerprogramm Skyplot (Version vom 1. 8. 1990). Er schreibt hierzu in seiner Anleitung:
Hier etwas zur Erklärung der Ephemeridenzeit: Die Erdrotation wird durch den Mond über die Gezeiten gebremst, so dass sich die Erde immer langsamer dreht. Deshalb nimmt die Länge eines Tages zu, etwa um zwei Tausendstel Sekunden pro Jahrhundert. Das mag sich wenig anhören, aber im Laufe der Zeit addieren sich die Differenzen immer mehr, so dass schon in einigen hundert oder tausend Jahren eine beträchtliche Differenz herauskommt. (Dazu kommen unregelmässige Effekte durch Verlagerung von Massen auf der Erde etc.)
Wenn man nun von heute an mit einem konstanten Zeitablauf zurückrechnet, wie Skyplot das normalerweise macht, stimmt die Stellung der Erde immer weniger. Will man zum Beispiel die Verlaufszone einer Sonnenfinsternis um Christi Geburt bestimmen, berechnet man die Position von Sonne und Mond, die ja von der Erdrotation unabhängig sind. Man erhält dann einen Zeitpunkt, der, nehmen wir einmal an, genau 727000 Tage zurückliegt. Wenn man von der heutigen Stellung der sich drehenden Erde ausgeht und eine ganze Zahl von Erdrotationen zurückrechnet, ist die damalige Stellung die gleiche und man glaubt, das Gebiet der Finsternis zu kennen.
Dabei ist man aber davon ausgegangen, dass sich die Erde immer gleich schnell dreht, was sie aber nicht tut. Zwar ist der absolute Zeitpunkt der Finsternis korrekt, aber die Erde hat sich zu diesem Zeitpunkt weiter gedreht als berechnet. Deshalb liegt der tatsächliche Verlauf der Finsternis weiter östlich als die Berechnungen glauben macht. Die Erde hat also KEINE ganzzahlige Anzahl von Umdrehungen in der Zwischenzeit gemacht.
Am 5. März 1223 v. Chr. fand in Nordafrika und im Nahen Osten eine totale Sonnenfinsternis statt, die Skyplot ohne die Zeitkorrektur als in Amerika stattfindend berechnet. Mit der Korrektur kommt die Zone korrekt heraus.
Das ist eine Differenz von über 10000 Kilometer, entsprechend fast siebeneinhalb Stunden, wenn man nur etwa 3000 Jahre zurückrechnet! Rechnet man noch weiter zurück oder in die Zukunft, so werden die Differenzen noch grösser. Für zukünftige Finsternisse liegt der tatsächliche Verlauf weiter im Westen als ohne Korrektur, da sich die Erde dann noch nicht so weit gedreht hat.
Normalerweise rechnet man mit der Weltzeit, die KEIN gleichmässiges Zeitmass ist. Manchmal wird am Jahresende oder in der Jahresmitte eine Schaltsekunde eingebaut, um die Weltzeit an die veränderliche Erdrotation zu koppeln. Die Ephemeridenzeit (oder verschiedene Atomzeitdefinitionen wie TDT und TDB, die ganz ähnlich sind) ist eine absolut gleichmässige Zeit, die am 31. Dezember 1900 mit der Weltzeit übereinstimmte. Inzwischen hat sich die Erdrotation aber verlangsamt, so dass jetzt eine Ephemeridenzeit anzeigende Uhr gegenüber der Weltzeit um fast eine Minute VORGEHT. Für Zeitpunkte vor 1900 geht die Ephemeridenzeit gegenüber der Weltzeit NACH.
Die Weltzeit wird so korrigiert, dass die Sonne immer etwa um 12 Uhr Ortszeit im Meridian steht, auch in Tausenden von Jahren (nach der Ephemeridenzeit wäre es irgendwann um 0 Uhr Mittag!)..........
Eine genaue Berechnung der Abweichung Ephemeridenzeit - Weltzeit kann nicht durchgeführt werden, da die Erdrotation nicht berechenbar ist, sondern von Klimawechseln etc. beeinflusst wird. Über grössere Zeiträume kann man deshalb nur interpolieren, Abweichungen gibt es immer.
Skyplot rechnete früher (....) mit einer Differenz DeltaT von N2 * 27.4 Sekunden, wobei N die Zeitdifferenz zu 1900 in Jahrhunderten ist. Der Wert war so gewählt, dass die oben erwähnte Finsternis im Jahre 1223 v. Chr. korrekt berechnet wurde.
Ein neuer Wert von N2 * 38.3 + N * 190.6 stammt aus dem Werk "Tidal Friction and the Earth´s Rotation" von P.Brosche und J. Sundermann (Springer-Verlag 1978) und wurde mir von Th. Pfleger mitgeteilt. [ 5 ]
Reingold und Dershowitz schreiben in ihren Calendrical Calculations auf Seite 170 zu diesem Problem: Astronomical calculations are typically done using Dynamical Time with its unchanging time units. (There are various forms of Dynamical Time, but the differences are too small to be of concern to us.) Solar time units, on the other hand, are not constant mainly because of the retarding effects of tides and the atmosphere, which cause a relatively steady lengthening of the day and contribute what is called a "secular" (that is, steadily changing) term to its length. This slowdown causes the mean solar day to increase in length by about 1.7 milliseconds per century. Because Universal Time is based on the Earth's speed of rotation, wich is slowly decreasing, the discrepancy between Universal and Dynamical Time is growing. It now stands at about 65 seconds and is currently increasing at about an average of 1 second per year. To account for the vagaries in the length of an astronomical day, every now and then a leap second is inserted (usually between December 31 and January 1, thereby keeping our clocks - which show Universal Time - in tune with the gradually slowing rotation of earth. Because the accumulated discrepancy is not entirely predictable, we use the following ad hoc function...[ 6 ]
Der genaue Wert der Akzeleration lässt sich wie gesagt nicht genau berechnen, und somit auch nicht die Differenz zwischen Ephemeridenzeit und Weltzeit. Für die Jahre von 1900 bis 1985 bietet Oliver Montenbruck[ 7 ] folgende Formel an, die eine recht genaue Näherung bringt:
DeltaT = ET - UT
DeltaT = ((( -339.84 sec * T - 516.52 sec) * T - 160.22 sec) * T) + 92.23 sec) * T + 71.28 sec
T: julianische Jahrhunderte, bezogen auf den 1. 1. 2000 (!), 12.00 Uhr
T = (JD - 2451545.0) / 36525 (-1.0 ≤ T ≤ -0.15)
Verlässt man allerdings den genannten Zeitraum, geht man insbesondere weiter in die Vergangenheit zurück, so wird die genannte Formel schnell ungenau. In diesem Fall soll die folgende Formel befriedigende Ergebnisse bieten:
DeltaT = 2.818 * 10-4 + 8.37 * 10-4 * T + 3.466* 10-4 * T2 + const.
ET = UT + DeltaT
T: julianische Jahrhunderte, bezogen auf den 1. 1. 1900 (!), 12.00 Uhr
T = (JD - 2415020.0) / 36525
DeltaT in Tagesbruchteilen
Diese Gleichung wurde entnommen dem Buch "Sterne im Computer" von Klaus Hempe und Jürgen Molt[ 8 ], wo sie folgendermassen kommentiert wird: "Die Konstante in (dieser) Gleichung ist zeitlich veränderlich und kann nur nachträglich für jedes Jahr aus den Beobachtungen der Planetenörter bestimmt werden. ..... Man kann die Gleichung ...... also nicht verwenden, wenn T kleiner ist. Diese Ephemeridenzeitkorrektur ist aber dann sinnvoll anwendbar, wenn Mond- und Planetenörter für Zeiten berechnet werden sollen, die weit in der Zukunft oder in der Vergangenheit liegen (T ist dann gross)."
Reingold gibt insgesamt vier verschiedene Formeln für die Jahre 1988 bis 2019, 1900 bis 1987, 1800 bis 1899, 1620 bis 1799 sowie für die Jahre vor 1620 oder nach 2020.
Für die Jahre vor 1620 verwendet er die Formel:
(x2 / 41048480 - 15) / (24 * 60 * 60) [x = JD(1. 1. 1810) - JD(1.1.Jahr) + 0.5]
Seine Formel für die Jahre 1620 bis 1799 fällt etwas aus dem Rahmen, dennoch dürften diese Berechnungen die genauesten der hier vorgestellten Möglichkeiten sein.
Den Unterschied zwischen Ephemeridenzeit und Weltzeit kann man auch aus den oben genannten Formeln zur Berechnung der Mittleren Sonnenlänge (nach Newcomb bzw. Ahnert) abzuleiten versuchen. Beide Formeln gehen vom gleichen Startwert aus. Der geringe Unterschied erklärt sich dadurch, dass Newcomb vom 0. Januar 1900, 12.00 Uhr ausgeht, Ahnert dagegen vom 0. Januar 1900, 0.00 Uhr (Weltzeit oder Ephemeridenzeit, zu diesem Zeitpunkt stimmen ja beide überein). Auch bei dem Wert für das tropische Jahr (bezogen auf 1900) stimmen beide überein. Im folgenden Term jedoch, dem Glied mit T2, das für die Akzeleration steht, gibt es einen deutlichen Unterschied. Dies lässt sich nur folgendermassen erklären: Newcomb´s Formel liegt ja die Ephemeridenzeit zugrunde. Sie berücksichtigt die Verlangsamung der Rotationsgeschindigkeit der Erde überhaupt nicht. Die scheinbare Beschleunigung der Sonne ist also ausschliesslich zu erklären aus der Beschleunigung der allgemeinen Präzession. Ahnert´s Formel hingegen berücksichtigt sowohl die Beschleunigung der Präzession wie auch die Verlangsamung der Erdrotation. Ob diese säkulär ist, also immer in die gleiche Richtung geht, oder ob es sich um eine periodische Schwankung, wenn auch mit einer sehr grossen Periode handelt, kann nicht gesagt werden. Ahnert schreibt hierzu etwas unklar (a.a.O., S. 9): "Die Grösse der Präzession ist nicht konstant, sie nimmt gegenwärtig zu und war in der Vergangenheit etwas geringer." Die Differenz die sich aus den Formeln von Newcomb und Ahnert ergibt, müsste also den Unterschied in der Sonnenlänge einmal mit und einmal ohne Berücksichtigung der Akzeleration zum Ergebnis haben und, wenn man 1 Grad in der Sonnenlänge gleich einem Tag setzt, ungefähr DeltaT ergeben:
DeltaT = (0.00065 - 0.0003025) * T2 = 0.0003475 * T2
oder, wenn man 360 Grad gleich 365.2422 Tage setzt:DeltaT = 0.00035256 * T2 (in Tagesbruchteilen)
Natürlich kann man auch aus der immer wieder zitierten Erkenntnis, dass die Tageslänge um 0.0016 Sekunden im Jahrhundert zunimmt, eine Formel für DeltaT entwickeln:
0.0016 Sekunden pro Jahrhundert entspricht 4.38-8 Sekunden pro Tag
4.38-8sec * (36525 + 365252) / 2 = 29.2208 sec
DeltaT = 29.2208 * T2 (in Sekunden)
Die folgende Grafik soll das Besprochene noch einmal verdeutlichen, sie basiert auf der Formel von Hempe und Molt.
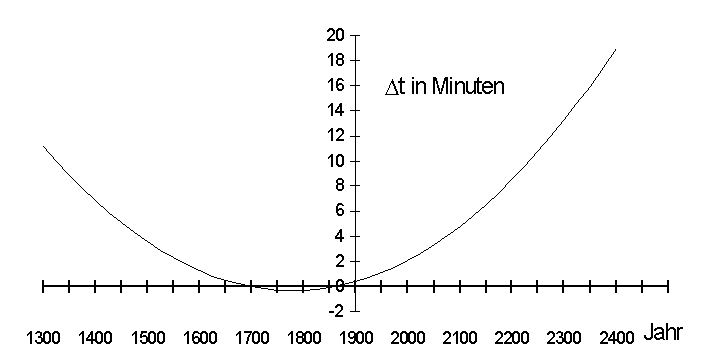
Eines zeigt diese Darstellung deutlich: DeltaT ist (fast immer) positiv. Dies kann man sich mit einer einfachen Überlegung klar machen (wozu allerdings der Schreiber dieser Zeilen lange brauchte): Geht man weit in die Vergangenheit zurück, so war einmal zu einem Zeitpunkt 12.00 Uhr ET gleich 11.00 Uhr UT. Da damals die Erde schneller rotierte, ging eine nach UT ausgerichtete Uhr gegenüber einer ET-Uhr schneller, ging also vor. Der Abstand zwischen ET und UT wurde immer geringer, bis 1900 dann beide Uhren gleich gingen. Von da ab ging dann aber die UT-Uhr langsamer als die ET-Uhr, ging also nach, so dass in ferner Zukunft einmal 12.00 Uhr ET wieder 11.00 Uhr UT entsprechen wird.
| |
|
Seitenanfang | Seitenende |
| 1 | nach Reingold-Dershowitz: | |||||||||||
| Vier unterschiedliche Formeln | ||||||||||||
| Dies ergibt folgende Abweichungen: | ||||||||||||
| 1900: | - 0 (!) Std. | 00 Min. | 02 Sec | 1920: | 0 Std. | 00 Min. | 22 Sec | |||||
| 1850: | 0 Std. | 00 Min. | 07 Sec | 1940: | 0 Std. | 00 Min. | 25 Sec | |||||
| 1800: | 0 Std. | 00 Min. | 14 Sec | 1960: | 0 Std. | 00 Min. | 34 Sec | |||||
| 1600: | 0 Std. | 02 Min. | 08 Sec | 1980: | 0 Std. | 00 Min. | 51 Sec | |||||
| 1000: | 0 Std. | 35 Min. | 15 Sec | 2000: | 0 Std. | 01 Min. | 07 Sec | |||||
| 1: | 2 Std. | 56 Min. | 54 Sec | 2200: | 0 Std. | 08 Min. | 01 Sec | |||||
| -2000: | 13 Std. | 05 Min. | 49 Sec | 3000: | 1 Std. | 16 Min. | 31 Sec | |||||
| -5000: | 41 Std. | 51 Min. | 24 Sec | 5000: | 9 Std. | 11 Min. | 06 Sec | |||||
| 2 | nach Hempe und Molt | |||||||||||
| DeltaT = 0.0002815 + 0.000837 * T + 0.0003466 * T2 (in Tagesbruchteilen) | ||||||||||||
| DeltaT = 24.3216 + 72.3168 * T + 29.94624 * T2 (in Sekunden) | ||||||||||||
| Dies ergibt folgende Abweichungen: | ||||||||||||
| 1900: | 0 Std. | 00 Min. | 25 Sec | 1920: | 0 Std. | 00 Min. | 40 Sec | |||||
| 1850: | - 0 (!)Std. | 00 Min. | 04 Sec | 1940: | 0 Std. | 00 Min. | 59 Sec | |||||
| 1800: | - 0 (!) Std. | 00 Min. | 01 Sec | 1960: | 0 Std. | 01 Min. | 19 Sec | |||||
| 1600: | 0 Std. | 01 Min. | 16 Sec | 1980: | 0 Std. | 01 Min. | 42 Sec | |||||
| 1000: | 0 Std. | 29 Min. | 57 Sec | 2000: | 0 Std. | 02 Min. | 07 Sec | |||||
| 1: | 2 Std. | 37 Min. | 25 Sec | 2200: | 0 Std. | 08 Min. | 32 Sec | |||||
| -2000: | 11 Std. | 52 Min. | 20 Sec | 3000: | 1 Std. | 14 Min. | 07 Sec | |||||
| -5000: | 38 Std. | 13 Min. | 07 Sec | 5000: | 20 Std. | 2 Min. | 07 Sec | |||||
| 3 | nach Thielen 1. Version | |||||||||||
| DeltaT = 0.000317129 * T2 (in Tagesbruchteilen) | ||||||||||||
| DeltaT = 27.4 * T2 in Sekunden) | ||||||||||||
| Dies ergibt folgende Abweichungen: | ||||||||||||
| 1900: | 0 Std. | 00 Min. | 00 Sec | 1920: | 0 Std. | 00 Min. | 01 Sec | |||||
| 1850: | 0 Std. | 00 Min. | 07 Sec | 1940: | 0 Std. | 00 Min. | 04 Sec | |||||
| 1800: | 0 Std. | 00 Min. | 27 Sec | 1960: | 0 Std. | 00 Min. | 10 Sec | |||||
| 1600: | 0 Std. | 04 Min. | 06 Sec | 1980: | 0 Std. | 00 Min. | 18 Sec | |||||
| 1000: | 0 Std. | 36 Min. | 57 Sec | 2000: | 0 Std. | 00 Min. | 28 Sec | |||||
| 1: | 2 Std. | 44 Min. | 35 Sec | 2200: | 0 Std. | 04 Min. | 07 Sec | |||||
| -2000: | 11 Std. | 34 Min. | 24 Sec | 3000: | 0 Std. | 55 Min. | 18 Sec | |||||
| -5000: | 36 Std. | 13 Min. | 51 Sec | 5000: | 7 Std. | 18 Min. | 59 Sec | |||||
| 4 | nach Thielen 2. Version | |||||||||||
| DeltaT = 0.002202546 * T + 0.000443287 * T2 (in Tagesbruchteilen) | ||||||||||||
| DeltaT = 190.6 * T + 38.3 * T2 (in Sekunden) | ||||||||||||
| Dies ergibt folgende Abweichungen: | ||||||||||||
| 1900: | 0 Std. | 00 Min. | 01 Sec | 1920: | 0 Std. | 00 Min. | 41 Sec | |||||
| 1850: | - 0 (!) Std. | 01 Min. | 02 Sec | 1940: | 0 Std. | 1 Min. | 23 Sec | |||||
| 1800: | - 0 (!) Std. | 02 Min. | 03 Sec | 1960: | 0 Std. | 02 Min. | 09 Sec | |||||
| 1600: | - 0 (!) Std. | 03 Min. | 47 Sec | 1980: | 0 Std. | 2 Min. | 58 Sec | |||||
| 1000: | 0 Std. | 23 Min. | 04 Sec | 2000: | 0 Std. | 03 Min. | 50 Sec | |||||
| 1: | 2 Std. | 49 Min. | 46 Sec | 2200: | 0 Std. | 15 Min. | 19 Sec | |||||
| -2000: | 14 Std. | 06 Min. | 46 Sec | 3000: | 1 Std. | 52 Min. | 16 Sec | |||||
| -5000: | 46 Std. | 59 Min. | 28 Sec | 5000: | 11 Std. | 52 Min. | 06 Sec | |||||
| 5 | Differenz der Sonnenlänge nach Newcomb und Ahnert | |||||||||||
| DeltaT = 0.00035256 * T2 (in Tagesbruchteilen) | ||||||||||||
| DeltaT = 30.4612 * T2 (in Sekunden) | ||||||||||||
| Dies ergibt folgende Abweichungen: | ||||||||||||
| 1900: | 0 Std. | 00 Min. | 00 Sec | 1920: | 0 Std. | 00 Min. | 01 Sec | |||||
| 1850: | 0 Std. | 00 Min. | 07 Sec | 1940: | 0 Std. | 00 Min. | 05 Sec | |||||
| 1800: | 0 Std. | 00 Min. | 30 Sec | 1960: | 0 Std. | 00 Min. | 11 Sec | |||||
| 1600: | 0 Std. | 04 Min. | 33 Sec | 1980: | 0 Std. | 00 Min. | 20 Sec | |||||
| 1000: | 0 Std. | 41 Min. | 04 Sec | 2000: | 00 Std. | 00 Min. | 31 Sec | |||||
| 1: | 3 Std. | 02 Min. | 59 Sec | 2200: | 0 Std. | 04 Min. | 35 Sec | |||||
| -2000: | 12 Std. | 51 Min. | 59 Sec | 3000: | 1 Std. | 01 Min. | 29 Sec | |||||
| -5000: | 40 Std. | 16 Min. | 43 Sec | 5000: | 7 Std. | 48 Min. | 09 Sec | |||||
| 6 | anhand der Feststellung: Verlängerung des Tages um 0.0016 Sekunden pro Jahrhundert |
|||||||||||
| DeltaT = 0.000338203 * T2 (in Tagesbruchteilen) | ||||||||||||
| DeltaT = 29.2208 * T2 (in Sekunden) | ||||||||||||
| Dies ergibt folgende Abweichungen: | ||||||||||||
| 1900: | 0 Std. | 00 Min. | 00 Sec | 1920: | 0 Std. | 00 Min. | 01 Sec | |||||
| 1850: | 0 Std. | 00 Min. | 07 Sec | 1940: | 0 Std. | 00 Min. | 05 Sec | |||||
| 1800: | 0 Std. | 00 Min. | 29 Sec | 1960: | 0 Std. | 00 Min. | 11 Sec | |||||
| 1600: | 0 Std. | 04 Min. | 22 Sec | 1980: | 0 Std. | 00 Min. | 19 Sec | |||||
| 1000: | 0 Std. | 39 Min. | 24 Sec | 2000: | 0 Std. | 00 Min. | 30 Sec | |||||
| 1: | 2 Std. | 55 Min. | 32 Sec | 2200: | 0 Std. | 04 Min. | 24 Sec | |||||
| -2000: | 12 Std. | 20 Min. | 33 Sec | 3000: | 0 Std. | 58 Min. | 59 Sec | |||||
| -5000: | 38 Std. | 38 Min. | 19 Sec | 5000: | 7 Std. | 48 Min. | 09 Sec | |||||
Hier nun noch ein Rechner, der DeltaT nach den genannten Kriterien für ein einzugebendes Jahr berechnet:
| |
|
Seitenanfang | Seitenende |
Viele Jahrhunderte lang bemühten sich Astronomen erfolglos, die durchschnittliche Dauer des tropischen Jahres zu berechnen. 1955 schufen sie das "astronomische" tropische Jahr, das als der Zeitraum definiert wurde, in dem die mittlere Länge der Sonne um 360° zunimmt. Dem Kalenderjahr liegt hingegen das "chronologische" tropische Jahr zugrunde, also der Zeitraum, der vergeht, bis die Sonne vom Frühlingspunkt, dem Schnittpunkt von Ekliptik und Himmelsäquator, wieder bis zu eben diesem Punkt gelangt. Infolge der Nutation schwankt der Frühlingspunkt im Raum hin und her und verschiebt sich um bis zu 17.24" bei einer Periode von ca. 18.6 Jahren. Kein Jahr ist daher dem anderen gleich. Lässt man diese kurzperiodischen Störungen unberücksichtigt, betrachtet man also nur die mittlere Länge des Jahres, so stellt man fest, dass auch sie sich im Laufe der Zeit ändert. Hierfür sind im wesentlichen zwei Ursachen massgebend:
Die Erde, die ja keine ideale Kugel ist, sondern eher als Rotationsellipsoid bezeichnet werden kann, dreht sich auf ihrer Bahn um die Sonne gleich einem Kreisel um ihre eigene Achse. Sonne und Mond üben dabei infolge ihrer Anziehungskräfte ein Drehmoment auf den Äquatorwulst der Erde aus mit dem Ziel einer Aufrichtung der Erdachse. Dem kann die Erde nach den physikalischen Gesetzen nicht nachgeben, sie weicht rechtwinklig aus, was zu einer Achsverlagerung führt. Die verlängerte Erdachse beschreibt demzufolge in ca. 26000 Jahren einen Kreis um den mittleren Himmelspol. Auch die Äquatorebene, auf der die Erdachse senkrecht steht, ändert daher ihre Lage im Raum. Da andererseits der Winkel zwischen Äquatorebene und Ekliptikebene nahezu konstant bleibt, führt dies zu einer kontinuierlichen Verschiebung des Schnittpunktes dieser beiden Ebenen und zwar entgegengesetzt zu der Bahnrichtung der Erde.
Der Wert dieser Präzession genannten Erscheinung beträgt ca. 1°24' pro Jahrhundert (allgemeine Präzession in der Länge) Er wird bei der Dauer des tropischen Jahres direkt berücksichtigt. Allerdings ist er nicht konstant sondern nimmt im Laufe der Zeit immer mehr zu. Dadurch kommt sozusagen der Frühlingspunkt der Sonne bei ihrem Lauf um die Erde immer etwas mehr entgegen, wodurch sich natürlich die Dauer des Umlaufs verkürzt.
Diese Beschleunigung beträgt ca. 1.11" * T2.
(T gleich julianische Jahrhunderte, bezogen auf den 0.1.1900)
Setzt man 360° gleich 365.2422 Tagen so bedeutet dies eine Verkürzung des Tropischen Jahres um 27.0278 sec * T2 oder um 0.0003128 Tage * T2.
Dies heisst anders ausgedrückt, dass das tropische Jahr infolge der Beschleunigung der Präzession ca. 0.5352 Sekunden pro Jahrhundert abnimmt (27.0278 / 5050 * 100).
Untersucht man die Dauer des Jahres und ihre Veränderung, so muss man natürlich von der bürgerlichen Zeit, also von der Sonnenzeit ausgehen, die wiederum abhängt von der Rotationsgeschwindigkeit der Erde. Da diese jedoch, wie oben ausführlich besprochen, immer mehr abnimmt, muss demzufolge auch die Dauer des Jahres immer geringer werden. Geht man davon aus, dass die Dauer des Tages in 100 Jahren um 0.0016 sec zunimmt, so beträgt diese Abnahme 0.0016 sec * 365.2422 gleich 0.58438 sec pro Jahrhundert. Dies entspricht einer Abnahme von 29.2208 sec * T2. Die verschiedenen Theorien über den genauen Wert der Akzeleration wurden ja oben besprochen.
Addiert man beide Ursachen der Verminderung der Jahresdauer, so kommt man zu folgenden Ergebnissen:
Abnahme des tropischen Jahres : ca. 1.12 sec pro Jahrhundert oder ca. 0000013 Tage pro Jahrhundert
Dies entspricht einer Verkürzung um den Wert: 56.54 sec * T2 oder 0.000654 Tage * T2
All die genannten Zahlen sind natürlich nur Näherungswerte. Eine exakte Vorhersage für die Zukunft ist nicht möglich und auch beim Rückrechnen in die Vergangenheit werden selbst bei grösstem Rechenaufwand Ungenauigkeiten bleiben. Für den (aus astronomischer Sicht) kleinen Zeitraum jedoch, der für Fragen der Chronologie eine Rolle spielt, mögen derartige Überlegungen nützlich sein um festzustellen, wie "genau" ein Kalender ist.
Legt man die oben gemachten Berechnungen zugrunde, so ergeben sich für die Lange des tropischen Jahres folgende Werte:
| Jahr | Dauer des tropischen Jahres | |||||||||
| - 10.000 | 365.2437524 | Tage | gleich | 365 d | 5 h | 51 m | 00.21 sec | |||
| - 5000 | 365.2430996 | Tage | gleich | " | " | " | 03.81 sec | |||
| 0 | 365.2424268 | Tage | gleich | " | " | 49 m | 07.41 sec | |||
| 325 | 365.2424044 | Tage | gleich | " | " | " | 03.74 sec | |||
| 622 | 365.2423656 | Tage | gleich | " | " | " | 00.39 sec | |||
| 1000 | 365.2423656 | Tage | gleich | " | " | 48 m | 59.16 sec | |||
| 1582 | 365.2422403 | Tage | gleich | " | " | " | 49.56sec | |||
| 1900 | 365.2421987 | Tage | gleich | " | " | " | 45.97sec | |||
| 2000 | 365.2421857 | Tage | gleich | " | " | " | 44.85sec | |||
| 3000 | 365.2420552 | Tage | gleich | " | " | " | 33.57sec | |||
| 5000 | 365.2417941 | Tage | gleich | " | " | " | 11.01sec | |||
| 10.000 | 365.2411413 | Tage | gleich | " | " | 47 m | 14.61sec | |||
Für die Abweichung bei Berechnungen mit und ohne Berücksichtigung der Veränderung der Jahresdauer ergeben sich beim Sonnenjahr folgende Werte:
| Zeitraum in Jahren | Abweichung | ||||
| 100 | 57 sec | ||||
| 1000 | 1 h | 34 m | 58 sec | ||
| 2000 | 6 h | 39 m | 52 sec | ||
| 3000 | 14 h | 14 m | 42 sec | ||
| 5000 | 39 h | 34 m | 10 sec | ||
| 10000 | 158 h | 16m | 40 sec | ||
Es soll noch einmal betont werden, dass den obigen Tabellen ein konstanter Wert (56.98 sec * T2 bzw. eine Abnahme von 1.128 sec pro Jahrhundert) zugrunde liegt. Wie oben ausgeführt ist dies jedoch nur eine ganz grobe Näherung. Es sollte hier nur gezeigt werden, dass jeder Kalender, der auf einem mathematischen Algorithmus beruht, auf Dauer nicht genau sein kann. Der gregorianische Kalender geht von einer Jahreslänge von 365.2425 Tagen aus, ein sicher ausreichend genauer Wert. Ob später einmal die klare und einfache Schaltregel ergänzt werden sollte um den Zusatz: "Alle Jahre, die durch 4000 ohne Rest teilbar sind, sind keine Schaltjahre", wird erst die ferne Zukunft zeigen.
| |
|
Seitenanfang | Seitenende |
Gleich wie beim Jahr gilt auch beim Monat, dass kein Monat den anderen gleich ist. Gerade die Mondbahn wird durch eine Vielzahl von Störungen beeinflusst, die eine Abweichung vom Mittelwert um über 14 Stunden bewirken können. Der mittlere Wert von Jahr und Monat lässt sich direkt aus den Formeln von Newcomb ableiten.
Von besonderer Bedeutung ist die Dauer des synodischen Monats und seine Veränderungen im Laufe der Jahrhunderte, da er ja die Grundlage nahezu aller lunaren Kalender bildet. Die genannten Daten beziehen sich auf das Jahr 1900. Wie oben ausgeführt ändert sich scheinbar die Geschwindigkeit der Sonne, bewirkt durch das Anwachsen der Präzession und die Verlangsamung der Erdrotation. Diese beiden Faktoren haben natürlich auch Einfluss auf die scheinbare Geschwindigkeit des Mondes, bei dem allerdings noch eine reelle Verlangsamung der Bahngeschwindigkeit hinzukommt.
Irgendwann Anfang Januar 1900 (nach Newcomb genau am 1. 1. 1900 um 6.14 Uhr ET) war (mittlerer) Neumond, das heisst, Sonne und Mond hatten gleiche Längen. Alle 29.5305887 Tage würde sich dieser Zustand wiederholen, wäre die Bahngeschwindigkeit von Sonne und Mond immer gleichbleibend. Nach 100 Jahre, also ca. 1238 synodischen Monate, hat sich die Sonne jedoch nach Newcomb bereits um 0.0003025 Grad über den theoretischen Rendevouspunkt hinweg weiter bewegt, während der Mond noch 0.001133 Grad vor diesem Punkte steht. Die Differenz beträgt also 0.0014355 Grad. Um diese Strecke zu überwinden braucht der Mond ca. 0.000109 Tage oder 9.41 Sekunden. Um diesen Betrag verlängert sich also akkumuliert die Dauer des synodischen Monats in 100 Jahren. Anders ausgedrückt heisst dies, in einem Jahrhundert verlängert sich die Dauer des Monats um 0.015 Sekunden oder 0.000000175 Tage [9.39 / (1237 + 12372) / 2 * 1237 = 0.015].
Newcomb geht von einer gleichmässigen Zeit aus. Unterstellt man, dass die Verlangsamung der Erdrotation eine Zunahme der Tageslänge um 0.0016 Sekunden im Jahrhundert bewirkt, so würde dies den synodischen Monat um 0.04725 Sekunden pro Jahrhundert verkürzen. Hieraus errechnet sich eine Abnahme des synodischen Monats um 0.0295 Sekunden im Jahrhundert.
Nach den von Ahnert verwendeten Formeln, die die Akzeleration berücksichtigen, eilt die Sonne in 100 Jahren um 0.00065° voraus, der Mond sogar um 0.00343°. Die Differenz beträgt 0.00278°. Um diese Strecke zurückzulegen benötigt der Mond ca. 18.229 Sekunden. Dies bedeutet eine Abnahme des Monats um 0.03 Sekunden oder 0.00000035 Tage im Jahrhundert.
Unterstellt man eine Abnahme des synodischen Monats von rund 0.03 Sekunden gleich 0.00000034 Tagen pro Jahrhundert so ergeben sich folgende Werte:
| Jahr | Dauer des synodischen Monats | ||||||||
| - 10000 | 29.5306300 | Tage | gleich | 29 d | 12 h | 44 m | 06.43 sec | ||
| - 5000 | 29.5306126 | Tage | gleich | " | " | " | 04.93 sec | ||
| 0 | 29.5305953 | Tage | gleich | " | " | " | 03.43 sec | ||
| 325 | 29.5305941 | Tage | gleich | " | " | " | 03.33 sec | ||
| 622 | 29.5305931 | Tage | gleich | " | " | " | 03.24 sec | ||
| 1000 | 29.5305892 | Tage | gleich | " | " | " | 03.13 sec | ||
| 1582 | 29.5305898 | Tage | gleich | " | " | " | 02.96sec | ||
| 1900 | 29.5305887 | Tage | gleich | " | " | " | 02.86sec | ||
| 2000 | 29.5305883 | Tage | gleich | " | " | " | 02.83sec | ||
| 5000 | 29.5305779 | Tage | gleich | " | " | " | 01.93sec | ||
| 10000 | 29.5305605 | Tage | gleich | " | " | " | 00.43sec | ||
| 11433 | 29.5305556 | Tage | gleich | " | " | " | 00.00sec | ||
Die Unterschiede, die sich bei Berechnungen mit und ohne Berücksichtigung der Verkürzung ergeben, zeigt die folgende Tabelle:
| Zeitraum in Jahren | Abweichung | ||||
| 100 | 18 sec | ||||
| 1000 | 30 m | 20 sec | |||
| 2000 | 2 h | 1 m | 30 sec | ||
| 3000 | 4 h | 33 m | 30 sec | ||
| 5000 | 12 h | 39 m | 30 sec | ||
| 10000 | 50 h | 38 m | 20 sec | ||
Auch bezüglich der Dauer des synodischen Monats gilt, dass es sich hier um rein theoretische Überlegungen handelt, die eine Tendenz aufzeigen wollen, die aber die wirkliche Entwicklung nicht genau wiedergeben.
| |
|
Seitenanfang | Seitenende |
[ 1 ] zitiert nach Montenbruck (1987).
[ 2 ] [Ahnert (1960)].
[ 3 ] Herrmann (1990)
[ 4 ] [Ahnert (1960)]
[ 5 ] Dieses (ursprünglich für Atari geschriebene) wunderschöne Programm von Herrn Thielen dürfte wohl nicht mehr erhältlich sein. Auch das Nachfolgeprogramm für Windows [Thielen (1996) ] ist inzwischen verramscht worden.
Nachtrag April 2004: Es gibt ein neues Skyplot von Thielen für Windows XP. siehe:
http://www.skyplot.de/. Dank an Herrn Pflanzer für diesen Hinweis.
[ 6 ] Reingold-Dershowitz (2001)
[ 7 ] Montenbruck (1987)
[ 8 ] Hempe-Molt (1986)
| |
Seitenanfang |
| Startseite | Glossar | Gästebuch | Forum | Impressum | FAQ | Inhalt |